题目内容
 如图,点A、B、C是⊙O上的三点,AB∥OC.
如图,点A、B、C是⊙O上的三点,AB∥OC.(1)求证:AC平分∠OAB.
(2)过点O作OE⊥AB于点E,交AC于点P.若AB=2,OE=
| 3 |
考点:垂径定理,勾股定理,圆周角定理
专题:
分析:(1)根据等腰三角形性质和平行线性质推出∠BAC=∠OAC即可;
(2)根据平行得出相似,根据相似得出比例式,代入求出即可.
(2)根据平行得出相似,根据相似得出比例式,代入求出即可.
解答:(1)证明:∵OC=OA,
∴∠C=∠OAC,
∵AB∥OC,
∴∠BAC=∠C,
∴∠BAC=∠OAC,
即AC平分∠OAB;
(2)解:∵OE⊥AB,AB=2,OE为半径,
∴AE=BE=1,
∵OE=
,
由勾股定理得:OA=2,
即OC=2,
∵AB∥OC,
∴△COP∽△AEP,
∴
=
,
∴
=
,
解得:PE=
.
∴∠C=∠OAC,
∵AB∥OC,
∴∠BAC=∠C,
∴∠BAC=∠OAC,
即AC平分∠OAB;
(2)解:∵OE⊥AB,AB=2,OE为半径,
∴AE=BE=1,
∵OE=
| 3 |
由勾股定理得:OA=2,
即OC=2,
∵AB∥OC,
∴△COP∽△AEP,
∴
| AE |
| OC |
| PE |
| OP |
∴
| 1 |
| 2 |
| PE | ||
|
解得:PE=
| ||
| 3 |
点评:本题考查了垂径定理,相似三角形的性质和判定,平行线的性质,等腰三角形的性质,勾股定理的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
相关题目
702班某兴趣小组有7名成员,他们的年龄(单位:岁)分别为:12,13,13,14,12,13,15,则他们年龄的众数和中位数分别为( )
| A、13,14 |
| B、14,13 |
| C、13,13 |
| D、13,13.5 |
下列四个数中的负数是( )
| A、-22 | ||
B、
| ||
| C、(-2)2 | ||
| D、|-2| |
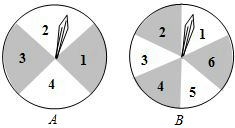 如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、5、6六个数字.有人为甲、乙两人设计了一个游戏,其规则如下:
如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、5、6六个数字.有人为甲、乙两人设计了一个游戏,其规则如下: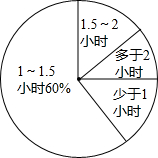 为进一步规范教育教学行为,切实减轻学生的课业负担,某校想了解本校九年级学生家庭作业用时情况.
为进一步规范教育教学行为,切实减轻学生的课业负担,某校想了解本校九年级学生家庭作业用时情况.
 如图,四边形ABCD为菱形,已知A(0,4),B(-3,0).
如图,四边形ABCD为菱形,已知A(0,4),B(-3,0).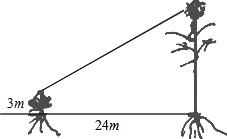 有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5.2m/s,那它至少需要多少时间才能赶回巢中?
有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m的一棵大树上,大树高14m,且巢离树顶部1m.当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5.2m/s,那它至少需要多少时间才能赶回巢中?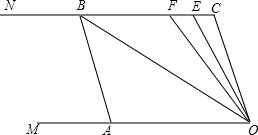 如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.
如图,已知两条射线OM∥CN,动线段AB的两个端点A、B分别在射线OM、CN上,且∠C=∠OAB=108°,F在线段CB上,OB平分∠AOF,OE平分∠COF.