题目内容
10．
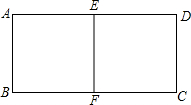如图，把一个矩形纸片ABCD沿AD和BC的中点连线EF对折，要使矩形AEFB与原矩形相似，则原矩形长与宽的比为（ ）| A． | 2：1 | B． | 3：1 | C． | $\sqrt{2}$：1 | D． | 4：1 |
分析 根据相似多边形对应边的比相等，设出原来矩形的长与宽，就可得到一个方程，解方程即可求得．
解答 解：根据条件可知：矩形AEFB∽矩形ABCD，
∴$\frac{AE}{AB}=\frac{AB}{AD}$，
设AD=x，AB=y，则AE=$\frac{1}{2}$x．则$\frac{\frac{1}{2}x}{y}$=$\frac{y}{x}$，即：$\frac{1}{2}$x2=y2．
∴$\frac{{x}^{2}}{{y}^{2}}$=2．
∴x：y=$\sqrt{2}$：1．
即原矩形长与宽的比为$\sqrt{2}$：1．
故选C．
点评 本题考查了相似多边形的性质，根据相似形的对应边的比相等，把几何问题转化为方程问题，正确分清对应边，以及正确解方程是解决本题的关键．
练习册系列答案
相关题目
5．经过矩形一组对边中点的直线把矩形分成相同的两个矩形，这两个矩形与原矩形的关系（ ）
| A． | 一定相似 | B． | 一定不相似 | C． | 不一定相似 | D． | 以上说法都不对 |
2．电信公司在某市推出无线市话小灵通，收费标准为：前3分钟（不足3分钟按3分钟计）为0.2元，3分钟后每分钟（不足1分钟按1分钟计）收0.1元，则一次通话时间x（x≥3）分钟，与这次通话的费用y（元）之间的函数关系式是（ ）
| A． | y=0.2x+0.1 | B． | y=0.1x | C． | y=0.1x-0.1 | D． | y=0.1x+0.5 |
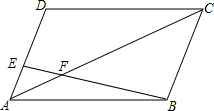如图，平行四边形ABCD中，AE：ED=1：2，S△AEF=6cm2，则S△CBF等于54cm2．