题目内容
18.完成下列各题(1)计算:$\frac{a}{a-b}$+$\frac{b}{b-a}$
(2)解不等式组$\left\{\begin{array}{l}{x-3<1}\\{4x-4≥x+2}\end{array}\right.$.
分析 (1)先通分,再把分子相加减即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答 解:(1)原式=$\frac{a}{a-b}$-$\frac{b}{a-b}$
=$\frac{a-b}{a-b}$
=1;
(2)$\left\{\begin{array}{l}x-3<1①\\ 4x-4≥x+2②\end{array}\right.$,由①得,x<4,由②得,x≥2,
故不等式组的解集为:2≤x<4.
点评 本题考查的是分式的加减法,熟知异分母的分式相加减的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列各组中,是二元一次方程x-5y=2的一个解的是( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ |
7.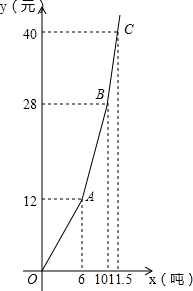 为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
(1)填空
价目表
(2)若某户居民9月份用水量为9.5吨,求该用户9月份水费;
(3)若某户居民10月份水费30元,求该用户10月份用水量;
(4)若某户居民11月、12月共用水18吨,其中11月用水a(吨),用含a的代数式表示该户居民11月、12月共应交水费Q(元).
 为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).
为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段以期待达到节水的目的,图是此区自来水厂对居民某月用水量x吨与水费y元的函数图象(水费按月结算).(1)填空
价目表
| 每月水用量 | 单价 |
| 不超出6吨的部分 | 2元/吨 |
| 超出6吨不超出10吨的部分 | 4 元/吨 |
| 超出10吨的部分 | 8元/吨 |
(3)若某户居民10月份水费30元,求该用户10月份用水量;
(4)若某户居民11月、12月共用水18吨,其中11月用水a(吨),用含a的代数式表示该户居民11月、12月共应交水费Q(元).
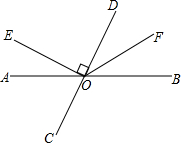 如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD.
如图,直线AB、CD相交于点O,OE⊥CD,OF平分∠BOD. 如图,在平行四边形ABCD中,∠A=120°,在AD上取DE=DC,求∠ECB的度数.
如图,在平行四边形ABCD中,∠A=120°,在AD上取DE=DC,求∠ECB的度数.


