题目内容
4.甲、乙两车分别从相距360km的 A、B两地出发,甲车速度为72km/h,乙车速度为48km/h.(1)两车同时出发,相向而行,两车何时相遇?
(2)两车同时出发,同向而行(乙车在前甲车在后),两车何时相遇?
(3)两车同时出发,同向而行,多长时间后两车相距120km?
分析 (1)根据相遇时,两车行驶的路程之和等于甲乙两地间的距离列方程求解即可;
(2)根据等量关系:乙车行驶的路程-甲车行驶的路程=两地间的距离列出方程求解即可;
(3)设ah后两车相距120km,然后分相遇前与相遇后两种情况列出方程求解即可.
解答 解:(1)设xh相遇,
由题意得,72x+48x=360,
解得x=3;
(2)设yh相遇,
由题意得,72y-48y=360,
解得y=15;
(3)设ah后两车相距120km,
若相遇前,则72a-48a=360-120,
解得a=10,
若相遇后,则72a-48a=360+120,
解得a=20,
答:10小时或20小时后两车相距120km.
点评 此题主要考查了一元一次方程的应用,主要利用了相遇问题等量关系,追及问题等量关系,熟练掌握行程问题的等量关系是解题的关键,难点在于(3)分情况讨论.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
14.下列方程中,是一元一次方程的是( )
| A. | x+y=2 | B. | x2=1 | C. | πx=2 | D. | $\frac{1}{x}$=1 |
19.下列说法正确的是( )
| A. | 近似数4.31万精确到0.01 | B. | 1.45×104精确到百位 | ||
| C. | 近似数4.60精确到十分位 | D. | 近似数5000万精确到个位 |
9.如图,从边长为(a+4)的正方形纸片中剪去一个边长为(a+1)的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )
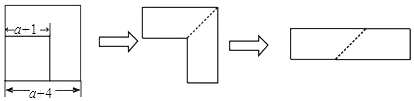

| A. | 3a+15 | B. | 6a+9 | C. | 2a2+5a | D. | 6a+15 |
13. 有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )
有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )
 有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )
有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )| A. | $\frac{a}{b}>0$ | B. | a-b>0 | C. | ab>0 | D. | a+b<0 |
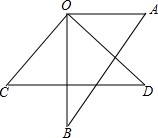 如图,已知∠COD=∠BOA=90°.
如图,已知∠COD=∠BOA=90°.