题目内容
15.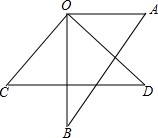 如图,已知∠COD=∠BOA=90°.
如图,已知∠COD=∠BOA=90°.(1)求证:∠AOD=∠BOC;
(2)求证:∠BOD+∠AOC=180°.
分析 (1)根据∠COD=∠BOA=90°可得∠COB+∠BOD=∠BOD+∠AOD,即可得证;
(2)由∠AOC=∠COD+∠AOD知∠BOD+∠AOC=∠BOD+∠COD+∠AOD=∠COD+∠AOB即可得证.
解答 证明:(1)∵∠COD=∠BOA=90°,
∴∠COB+∠BOD=∠BOD+∠AOD,
∴∠AOD=∠BOC;
(2)∵∠AOC=∠COD+∠AOD,
∴∠BOD+∠AOC=∠BOD+∠COD+∠AOD=∠COD+∠AOB,
又∵∠COD=∠BOA=90°,
∴∠BOD+∠AOC=180°.
点评 本题主要考查同角的余角相等,熟练掌握补、余角性质:等角的补角相等.等角的余角相等是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知弦AB把圆周分成2:3的两部分,则弧$\widehat{AB}$所对圆心角的度数是( )
| A. | 72° | B. | 72°或144° | C. | 144° | D. | 144°或216° |
6.某路口南北方向信号灯的设置时间为:红灯25s,绿灯30s,黄灯5s.王老师随机地由南往北开车到达该路口,他遇到绿灯的概率是( )
| A. | $\frac{6}{11}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{2}$ |
7.下列说法正确的是( )
| A. | 由5m=6m+2可得m=2 | |
| B. | 方程的解就是方程中未知数所取的值 | |
| C. | 方程2x-1=3的解是x=2 | |
| D. | 方程x=-x没有解 |
5.与-2ab是同类项的为( )
| A. | -2ac | B. | $\frac{{2{x^2}y}}{3}$ | C. | ab | D. | -2abc |
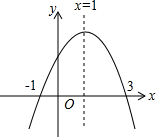 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①2a+b=0;②a+b+c>0;③当-1<x<3时,y>0;④-a+c<0.其中正确的个数为( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①2a+b=0;②a+b+c>0;③当-1<x<3时,y>0;④-a+c<0.其中正确的个数为( ) 用小立方块搭一个几何体,如图所示,这样的几何体最少需要9个小立方块,最多需要13个小立方块.
用小立方块搭一个几何体,如图所示,这样的几何体最少需要9个小立方块,最多需要13个小立方块.