题目内容
2.计算:($\frac{x+8}{{x}^{2}-4}$-$\frac{2}{x-2}$)÷$\frac{x-4}{{x}^{2}-4x+4}$•($\frac{x+8}{{x}^{2}-4}$-$\frac{2}{x}$).分析 首先对括号内的式子通分相减,把除法转化为乘法,然后进行约分即可.
解答 解:原式=$\frac{x+8-2(x+2)}{(x+2)(x-2)}$•$\frac{(x-2)^{2}}{x-4}$•$\frac{x+8-2({x}^{2}-4)}{(x+2)(x-2)}$
=$\frac{4-2x}{(x+2)(x-2)}$•$\frac{(x-2)^{2}}{x-4}$•$\frac{-2{x}^{2}+x+16}{(x+2)(x-2)}$
=$\frac{-2(x-2)}{(x+2)(x-2)}$•$\frac{(x-2)^{2}}{x-4}$•$\frac{-2{x}^{2}+x+16}{(x+2)(x-2)}$
=$\frac{-2(-2{x}^{2}+x+16)(x-2)}{(x+2)^{2}(x-4)}$.
点评 本题考查分式的混合运算,正确对分式进行通分、分母和分子分解因式是关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
7.已知|a|=4,|b|=3,|a+b|=-(a+b),则a-b=( )
| A. | -7 | B. | -1 | C. | -7或-1 | D. | ±7或±1 |

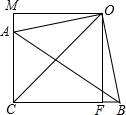 如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作等腰Rt△ABO,AC=5,OC2=72,过点O作OF⊥BC于F,AM⊥OM于M,OM=CF.
如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作等腰Rt△ABO,AC=5,OC2=72,过点O作OF⊥BC于F,AM⊥OM于M,OM=CF.