题目内容
 如图,已知,∠B=∠C=90°,点E是BC边上的中点,DE平分∠ADC,结论:①AE平分∠DAB;②AE⊥DE;③AE=DE;④S梯形ABCD=
如图,已知,∠B=∠C=90°,点E是BC边上的中点,DE平分∠ADC,结论:①AE平分∠DAB;②AE⊥DE;③AE=DE;④S梯形ABCD=| 1 |
| 2 |
(1)你认为正确的结论是
(2)选择你认为正确的一个结论证明.
考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:(1)过E作EF⊥AD,则可得EC=EF=BE,根据角平分线的判定可判定①正确,再根据角平分线的定义可判定②正确,根据面积可判定④⑤正确,可得到答案;
(2)可选①,利用角平分线的判定证明即可.
(2)可选①,利用角平分线的判定证明即可.
解答:解:(1)如图,过E作EF⊥AD于点F,

∵DE平分∠ADC,∠C=90°,
∴EC=EF,
又∵E为BC中点,
∴EF=BE,
∵∠B=90°,
∴BE⊥AB,
∴AE平分∠DAB,
∴①正确;
∵∠C=∠B,
∴AB∥CD,
∴∠CDA+∠BAD=180°,
∴2∠CAD+2∠ADE=180°,
∴∠CAD+∠ADE=90°,
∴∠AED=90°,即AE⊥DE,
∴②正确;
∴若AE=DE则∠EDA=∠EDC=45°,则∠ADC=90°,与条件不相符合,
∴③不正确;
在△CED和△FED中,
,
∴△CED≌△FED(AAS),
同理可得△AEF≌△AEB,
∴S梯形ABCD=2(S△EFD+S△EFA)=2S△AED,
∴⑤正确;
又S△AED=
AD•EF,EF=
BC,
∴S梯形ABCD=AD•EF=
AD•BC,
∴④正确;
综上可知正确的为①②④⑤,
故答案为:①②④⑤;
(2)选①证明:
如图,过E作EF⊥AD于点F,

∵DE平分∠ADC,∠C=90°,
∴EC=EF,
又E为BC中点,
∴EF=BE,
∵∠B=90°,
∴BE⊥AB,
∴AE平分∠DAB.

∵DE平分∠ADC,∠C=90°,
∴EC=EF,
又∵E为BC中点,
∴EF=BE,
∵∠B=90°,
∴BE⊥AB,
∴AE平分∠DAB,
∴①正确;
∵∠C=∠B,
∴AB∥CD,
∴∠CDA+∠BAD=180°,
∴2∠CAD+2∠ADE=180°,
∴∠CAD+∠ADE=90°,
∴∠AED=90°,即AE⊥DE,
∴②正确;
∴若AE=DE则∠EDA=∠EDC=45°,则∠ADC=90°,与条件不相符合,
∴③不正确;
在△CED和△FED中,
|
∴△CED≌△FED(AAS),
同理可得△AEF≌△AEB,
∴S梯形ABCD=2(S△EFD+S△EFA)=2S△AED,
∴⑤正确;
又S△AED=
| 1 |
| 2 |
| 1 |
| 2 |
∴S梯形ABCD=AD•EF=
| 1 |
| 2 |
∴④正确;
综上可知正确的为①②④⑤,
故答案为:①②④⑤;
(2)选①证明:
如图,过E作EF⊥AD于点F,

∵DE平分∠ADC,∠C=90°,
∴EC=EF,
又E为BC中点,
∴EF=BE,
∵∠B=90°,
∴BE⊥AB,
∴AE平分∠DAB.
点评:本题主要考查角平分线的性质和判定,掌握角平分线上的点到角两边的距离相等是解题的关键.注意全等三角形的判定和性质的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
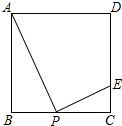 如图,在正方形ABCD中,点E在CD上,CE=
如图,在正方形ABCD中,点E在CD上,CE=