题目内容
16.已知x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,求x2+xy+y2的值.分析 根据二次根式的加减法法则、平方差公式求出x+y、xy,利用完全平方公式把所求的代数式变形,代入计算即可.
解答 解:∵x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,
∴x+y=($\sqrt{3}$+1)+($\sqrt{3}$-1)=2$\sqrt{3}$,xy=($\sqrt{3}$+1)($\sqrt{3}$-1)=2,
∴x2+xy+y2=x2+2xy+y2-xy=(x+y)2-xy=10.
点评 本题考查的是二次根式的化简求值,掌握二次根式的性质、二次根式的混合运算法则、完全平方公式、平方差公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.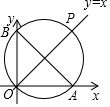 如图,平面直角坐标系中,A、B两点的坐标分别为(6,0)、(0,8),以AB为直径的圆与直线y=x交于点P,则点P的坐标是( )
如图,平面直角坐标系中,A、B两点的坐标分别为(6,0)、(0,8),以AB为直径的圆与直线y=x交于点P,则点P的坐标是( )
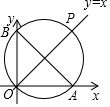 如图,平面直角坐标系中,A、B两点的坐标分别为(6,0)、(0,8),以AB为直径的圆与直线y=x交于点P,则点P的坐标是( )
如图,平面直角坐标系中,A、B两点的坐标分别为(6,0)、(0,8),以AB为直径的圆与直线y=x交于点P,则点P的坐标是( )| A. | (6.5,6.5) | B. | (7,7) | C. | (7.5,7.5) | D. | (8,8) |
4.下列等式由左边到右的变形中,属于因式分解的是( )
| A. | mx+nx+k=(m+n)x+k | B. | x2-9=(x+3)(x-3) | ||
| C. | x2-4+3x=(x+2)(x-2)-3x | D. | (a+b)(a-b)=a2-b2 |
1.在早餐店里,王伯伯买5个馒头,3个包子,老板少拿2元,只要50元.李太太买了11个馒头,5个包子,老板以售价的九折优待,只要90元.若馒头每个x元,包子每个y元,则下列可表示题目中的数量关系的二元一次方程组为( )
| A. | $\left\{\begin{array}{l}{5x+3y=50+2}\\{11x+5y=90×0.9}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x+3y=50+2}\\{11x+5y=90÷0.9}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+3y=50-2}\\{11x+5y=90×0.9}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x+3y=50-2}\\{11x+5y=90÷0.9}\end{array}\right.$ |
6.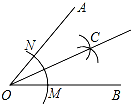 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )| A. | AAS | B. | ASA | ||
| C. | SSS | D. | 角平分线上的点到角两边距离相等 |