题目内容
16.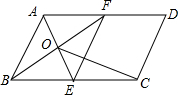 如图,在?ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.
如图,在?ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.(1)求证:四边形ABEF是菱形;
(2)若BC=8,∠ABC=60°,求OC的长.
分析 (1)根据邻边相等的平行四边形是菱形即可证明;
(2)过点O作OG⊥BC于点G.分别在Rt△OEG,Rt△OCG中解直角三角形即可;
解答 (1)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
∵E,F分别是BC,AD的中点,
∴$BE=\frac{1}{2}BC,AF=\frac{1}{2}AD$.
∴BE=AF.
∴四边形ABEF是平行四边形.
∵BC=2AB,
∴AB=BE.
∴平行四边形ABEF是菱形.
(2)解:过点O作OG⊥BC于点G.
∵E是BC的中点,BC=8,
∴BE=CE=4.
∵四边形ABEF是菱形,∠ABC=60°,
∴∠OBE=30°,∠BOE=90°.
∴OE=2,∠OEB=60°.
∴GE=1,OG=$\sqrt{3}$.
∴GC=5.
∴OC=$2\sqrt{7}$.
点评 本题考查平行四边形的性质、菱形的判定和性质、解直角三角形、拯救世界30度角性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
6.某班A、B、C、D、E五名同学进行跳棋比赛,每两名同学要进行两盘比赛,比赛结果没有平局,最后按积分多少排列名次,比赛中途积分记录表记录如下:
(1)由B和C的比赛成绩列方程计算出胜一盘的积分和负一盘的积分;
(2)表中a、b、c的数据是多少(直接写出结果)
a=2,b=1,c=13.
(3)若比赛全部结束,D的积分不少于A的积分,则后阶段的比赛中,D至少要胜几盘?
| 盘数 | 胜盘数 | 负盘数 | 积分 | |
| A | 8 | 4 | 4 | 32 |
| B | 5 | 3 | 2 | 21 |
| C | 6 | 2 | 4 | 22 |
| D | 3 | a | b | c |
| E | 6 | 3 | 3 | 24 |
(2)表中a、b、c的数据是多少(直接写出结果)
a=2,b=1,c=13.
(3)若比赛全部结束,D的积分不少于A的积分,则后阶段的比赛中,D至少要胜几盘?
11. 实数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
 实数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
实数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )| A. | a<-2 | B. | b>-1 | C. | -a<-b | D. | a>|b| |
 如图所示的几何体是由五个相同的小立方体组合而成的,则它的主视图是( )
如图所示的几何体是由五个相同的小立方体组合而成的,则它的主视图是( )



 如图,四边形OABC是面积为9的正方形,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.
如图,四边形OABC是面积为9的正方形,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.