题目内容
4. 如图,四边形OABC是面积为9的正方形,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.
如图,四边形OABC是面积为9的正方形,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.(1)求反比例函数的解析式;
(2)将正方形OABC分别沿直线AB、BC翻折,得到正方形MABC′、NA′BC,设线段MC′、NA′分别与函数y=$\frac{k}{x}$(x>0)的图象交于点E、F,求线段EF所在直线的解析式y1;
(3)当y1>y时,请直接写出x的取值范围.
分析 (1)由正方形的面积可求得B点坐标,利用待定系数法可求得反比例函数的解析式;
(2)由折叠的性质可求得E、F的坐标,利用待定系数法可求得直线EF的解析式;
(3)结合图象可求得答案.
解答 解:
(1)∵四边形OABC是面积为9的正方形,
∴OA=OC=3,
∴点B坐标为(3,3),
将x=3,y=3代入反比例函数解析式得k=xy=3×3=9
∴反比例函数的解析式为y=$\frac{9}{x}$;
(2)∵正方形MABC′、NA′BC由正方形OABC翻折所得,
∴ON=OM=2OA=6,
∴点E横坐标为6,点F纵坐标为6.
∵点E、F在函数y=$\frac{9}{x}$的图象上,
∴当x=6时,y=$\frac{3}{2}$,即E(6,$\frac{3}{2}$),
当y=6时,x=$\frac{3}{2}$,即F($\frac{3}{2}$,6),
设直线EF解析式为y1=mx+n,将E、F两点坐标代入,得$\left\{\begin{array}{l}{6m+n=\frac{3}{2}}\\{\frac{3}{2}m+n=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{n=\frac{15}{2}}\end{array}\right.$,
∴直线EF的解析式为y1=-x+$\frac{15}{2}$;
(3)当y1>y时,即直线在反比例函数图象的上方时所对应的自变量的取值范围,
∴当y1>y时,$\frac{3}{2}$<x<6.
点评 本题为反比例函数的综合应用,涉及待定系数法、正方形的性质、折叠的性质、数形结合思想等知识.在(1)中求得B点坐标是解题的关键,在(2)中求得E、F的坐标是解题的关键,在(3)中注意数形结合思想的应用.本题考查知识点较多,综合性较强,难度适中.

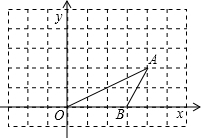 如图,点O、A、B的坐标分别为(0,0),(4,2),(3,0),将△OAB绕点O按逆时针方向旋转90°得到△OA′B′.
如图,点O、A、B的坐标分别为(0,0),(4,2),(3,0),将△OAB绕点O按逆时针方向旋转90°得到△OA′B′.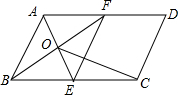 如图,在?ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.
如图,在?ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.