题目内容
12．如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第9个图形需要黑色棋子的个数是99．
分析 结合图形，发现：第1个图形中黑色棋子的个数是2×3-3；第2个图形中黑色棋子的个数是3×4-4；依此类推即可求解．
解答 解：第1个图形是2×3-3，第2个图形是3×4-4，第3个图形是4×5-5，
按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是（n+1）（n+2）-（n+2）=n2+2n，
当n=9时，92+2×9=99，
故第9个图形需要黑色棋子的个数是99（个）．
故答案为：99．
点评 考查了图形的变化类问题，首先计算几个特殊图形，发现：数出每边上的个数，乘以边数，但各个顶点的重复了一次，应再减去
练习册系列答案
相关题目
如图，四边形ABCD为平行四边形，CE∥BD，EF⊥AB交BA的延长线于点F，点E，D，A在一条直线上，试证明DF=$\frac{1}{2}$AE．
如图，5个一样大小的小矩形拼成一个大的矩形，如果大矩形的周长为14cm，则小矩形的周长为6cm．
20．
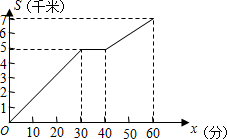一名学生骑自行车沿笔直的公路出行，这名同学离开起点的距离y（单位：千米）与行驶的时间x（单位：分）图象如图所示，则下面的结论中正确的是（ ）
一名学生骑自行车沿笔直的公路出行，这名同学离开起点的距离y（单位：千米）与行驶的时间x（单位：分）图象如图所示，则下面的结论中正确的是（ ）| A． | 整个过程的平均速度是$\frac{7}{60}$千米/时 | B． | 该同学途中停了10分钟 | ||
| C． | 前20分钟的速度比后20分钟慢 | D． | 从起点到终点共用了50分钟 |
如图，三角形ABC在直角坐标系中，其中A（-1，-1）．
如图，计算三角尺阴影部分的面积为$\frac{1}{2}$ab-πr2．
2．下列不等式中是一元一次不等式的是（ ）
| A． | m＜-m | B． | x-1≤y | C． | x2-x-3≥0 | D． | a+b＞c |