题目内容
12.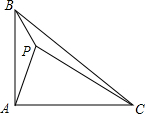 在△ABC中,∠BAC=90°,AB=AC,P是△ABC内一点,PA=2,PB=1,PC=3,求∠APB的度数.
在△ABC中,∠BAC=90°,AB=AC,P是△ABC内一点,PA=2,PB=1,PC=3,求∠APB的度数.
分析 由于∠ABC=90°,BC=AB,则可以把△PAC绕B点逆时针旋转90°得到△DBA,根据旋转的性质得到AD=AP=2,BD=PC=3,∠PBD=90°,得到△APD为等腰直角三角形,根据等腰直角三角形的性质得到PD=$\sqrt{2}$PA=2$\sqrt{2}$,∠DPB=45°,根据勾股定理的逆定理证明△BPD为直角三角形,然后利用∠APB=∠APD+∠DPB计算即可.
解答 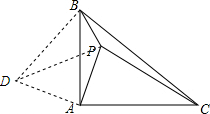 解:∵∠ABC=90°,BC=AB,
解:∵∠ABC=90°,BC=AB,
∴把△PAC绕A点逆时针旋转90°得到△DBA,如图,
∴BD=PC=3,AD=AP=2,∠PAD=90°,
∴△PAD为等腰直角三角形,
∴DP=$\sqrt{2}$PA=2$\sqrt{2}$,∠DPA=45°,
在△BPD中,PB=2,PD=2$\sqrt{2}$,DB=3,
∵12+(2$\sqrt{2}$)2=32,
∴AP2+PD2=BD2,
∴△BPD为直角三角形,
∴∠BPD=90°,
∴∠APB=∠APD+∠DPB=90°+45°=135°.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等腰直角三角形的性质以及勾股定理的逆定理.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
3.有如图所示的几种几何体:

将它们按截面形状分成两类时,下面的分法不正确的是( )

将它们按截面形状分成两类时,下面的分法不正确的是( )
| A. | 截面可能是圆和三角形两类 | B. | 截面可能是圆和四边形两类 | ||
| C. | 截面可能是圆和五边形两类 | D. | 截面可能是三角形和四边形两类 |
4.函数y=$\frac{m(m-3)}{x}$是反比例函数,则m必须满足( )
| A. | m≠3 | B. | m≠0或m≠3 | C. | m≠0 | D. | m≠0且m≠3 |
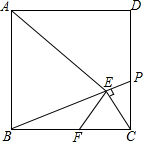 正方形ABCD中,AB=8,点P是CD上的一点,CE⊥BP垂足为E,EF⊥AE与边BC交于点F
正方形ABCD中,AB=8,点P是CD上的一点,CE⊥BP垂足为E,EF⊥AE与边BC交于点F 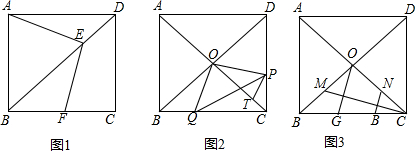




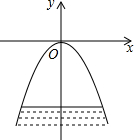 如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.
如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.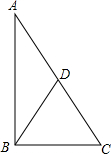 如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.
如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.