题目内容
一次函数y=kx+b的图象与y轴的交点为(0,5),且直线与两坐标轴围成的三角形面积为10,则一次函数的表达式为 .
考点:待定系数法求一次函数解析式
专题:
分析:先求出直线与坐标轴的交点,再根据三角形的面积公式求解即可.
解答:解:∵一次函数y=kx+b的图象与y轴的交点为(0,5),
∴b=5,
∴y=kx+5,
∴当y=0时,kx+5=0,解得x=-
,
∴一次函数y=kx+b的图象与坐标轴的交点分别为(0,5),(-
,0).
∵直线与两坐标轴围成的三角形面积为10,
∴
×5|-
|=10,
解得k=±
,
∴一次函数的表达式为y=
x+5或y=-
x+5.
故答案为:y=
x+5或y=-
x+5.
∴b=5,
∴y=kx+5,
∴当y=0时,kx+5=0,解得x=-
| 5 |
| k |
∴一次函数y=kx+b的图象与坐标轴的交点分别为(0,5),(-
| 5 |
| k |
∵直线与两坐标轴围成的三角形面积为10,
∴
| 1 |
| 2 |
| 5 |
| k |
解得k=±
| 5 |
| 4 |
∴一次函数的表达式为y=
| 5 |
| 4 |
| 5 |
| 4 |
故答案为:y=
| 5 |
| 4 |
| 5 |
| 4 |
点评:本题考查的是待定系数法求一次函数解析式,一次函数图象上点的坐标特点,三角形的面积,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法中,错误的是( )
| A、邻补角的角平分线互相垂直 |
| B、平行于同一直线的两条直线互相平行 |
| C、在同一平面内不相交的两条直线一定平行 |
| D、经过一点有且只有一条直线与已知直线平行 |
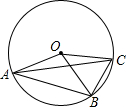 如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是( )
如图,OA,OB,OC都是⊙O的半径,若∠AOB是锐角,且∠AOB=2∠BOC.则下列结论正确的是( )| A、AB=2BC |
| B、AB<2BC |
| C、∠AOB=2∠CAB |
| D、∠ACB=4∠CAB |
将下列平面图形绕轴旋转一周,可得到圆锥的是( )
A、 |
B、 |
C、 |
D、 |
已知关于x的方程2x+2m=5的解是x=-2,则m的值为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.求线段EC的长度.
如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.求线段EC的长度. 如图,在⊙O中,弦AB长为l0,圆心O到AB的距离OD=12,则tan∠AOD的值为
如图,在⊙O中,弦AB长为l0,圆心O到AB的距离OD=12,则tan∠AOD的值为 如图,一艘渔船正以30海里/小时的速度由西向东追赶鱼群,在A处看小岛C在船北偏东60°方向,40分钟后渔船行驶至B处,此时看见小岛C在船北偏东30°方向.已知以小岛C为中心周围18海里的范围是有暗礁的危险区.
如图,一艘渔船正以30海里/小时的速度由西向东追赶鱼群,在A处看小岛C在船北偏东60°方向,40分钟后渔船行驶至B处,此时看见小岛C在船北偏东30°方向.已知以小岛C为中心周围18海里的范围是有暗礁的危险区. 如图所示,花都区某学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙为19m),另外三边利用学校现有总长38m的铁栏围成.若围成的面积为180m2,试求出自行车车棚的长和宽.
如图所示,花都区某学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙为19m),另外三边利用学校现有总长38m的铁栏围成.若围成的面积为180m2,试求出自行车车棚的长和宽.