题目内容
3.(1)先化简,再求值:(1-$\frac{3}{x+2}$)÷$\frac{{x}^{2}-1}{2x+4}$,其中x=3(2)若关于x的分式方程$\frac{2x+a}{x-2}=-1$的解是正数,求a的取值范围.
分析 (1)根据运算顺序,先算括号里面的,再算除法即可;
(2)先解方程,再使x的值>0且x≠2即可得出a的取值范围.
解答 解:(1)原式=$\frac{x+2-3}{x+2}$•$\frac{2(x+2)}{(x+1)(x-1)}$
=$\frac{2}{x+1}$,
∵x=3,
∴原式=$\frac{2}{x+1}$,
=$\frac{2}{3+1}$
=$\frac{1}{2}$;
(2)去分母得,2x+a=2-x,
移项得,2x+x=2-a,
合并得,3x=2-a,
系数化为1得,x=$\frac{2-a}{3}$,
∵关于x的分式方程$\frac{2x+a}{x-2}=-1$的解是正数,
∴x>0,即$\frac{2-a}{3}$>0,
解得a<2,
∵x≠2,∴$\frac{2-a}{3}$≠2,
∴a≠-4,
∴a的取值范围a<2且a≠-4.
点评 本题考查了分式的化简求值、分式方程的解,掌握分式有意义的条件分母不为0是解题的关键.

练习册系列答案
相关题目
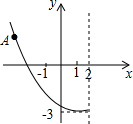 如图,二次函数y=ax2+bx+c的图象的一部分,已知A(-2.5,2),则根据图象可得到下列结论:
如图,二次函数y=ax2+bx+c的图象的一部分,已知A(-2.5,2),则根据图象可得到下列结论: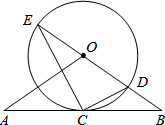 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.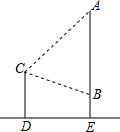 如图所示,小明、小军、小丽三个同学家正好住在一个小区,小军和小丽家在同一栋楼AE里,高度相差AB为(42+14$\sqrt{3}$)米,小明家在他们相对的一栋楼CD上,一日,小明站在自家阳台C处,发现小军家住A处,且仰角为45°,而小丽家在B处,俯角为30°,小丽家离地面高度BE=6米,试求两栋楼之间的距离DE及小明家离地面的高度CD($\sqrt{3}$=1.73,结果精确到0.01)
如图所示,小明、小军、小丽三个同学家正好住在一个小区,小军和小丽家在同一栋楼AE里,高度相差AB为(42+14$\sqrt{3}$)米,小明家在他们相对的一栋楼CD上,一日,小明站在自家阳台C处,发现小军家住A处,且仰角为45°,而小丽家在B处,俯角为30°,小丽家离地面高度BE=6米,试求两栋楼之间的距离DE及小明家离地面的高度CD($\sqrt{3}$=1.73,结果精确到0.01)