题目内容
7.某市为了解初中学生体能情况,抽取了50名初中毕业的女学生进行“一分钟仰卧起坐”次数测试,测试的情况绘制成表格如下:| 次数 | 6 | 12 | 15 | 18 | 20 | 25 | 27 | 30 | 32 | 35 | 36 |
| 人数 | 1 | 2 | 8 | 16 | 10 | 5 | 1 | 2 | 1 | 1 | 3 |
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少.
分析 (1)根据出现最多的是众数,把这组数据按大小关系排列,中间位置的是中位数(偶数个数据取中间两个数的平均值);平均数是总成绩除以次数;
(2)根据中位数或众数比较接近大部分学生成绩,故中位数或众数作为合格标准次数较为合适;
(3)根据50人中,有39人符合标准,进而求出合格率即可.
解答 解:(1)根据总数据有50个,第25,26个数据的平均数是中位数,故中位数为(18+18)÷2=18(次),
出现最多的是18次,故众数为18次,
平均数为:(6+12+15×8+18×16+20×10+25×5+27+30+32+35+36×3)÷50=20.5(次).
(2)用中位数或众数(18次)作为合格标准次数较为合适,
因为18次大部分同学都能达到,合格人数多.
(3)根据18次作为合格标准,50人中有50-1-2-8=39人合格,
合格率是39÷50=78%.
点评 此题主要考查了平均数、中位数和众数的定义以及利用样本估计总体,熟练掌握中位数和众数的定义以及平均数的计算方法解答是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下面说法中①零是最小的整数;②平方等于本身的数只有1;③若|2a|=-2a,则2a一定是负数;④m+|m|的结果必为非负数;⑤-a一定是一个负数,其中错误的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
12.用火柴棒按如图的方式搭建:
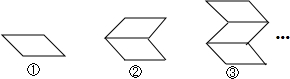
(1)填写表中:
(2)第n个图形需要多少根火柴棒?
(3)分别求出第15,21,55个图形时,需要多少根火柴棒?

(1)填写表中:
| 图形编号 | ① | ② | ③ | ④ | ⑤ | ⑥ |
| 火柴棒的根数 | 4 | 7 | 10 | 13 | 16 | 19 |
(3)分别求出第15,21,55个图形时,需要多少根火柴棒?
16.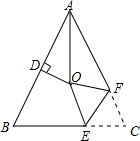 如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )
如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )
 如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )
如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为( )| A. | 50° | B. | 45° | C. | 65° | D. | 30° |
17.三角形两边长分别是8和6,第三边长是一元二次方程x2-16x+60=0一个实数根,则该三角形的面积是( )
| A. | 24 | B. | 48 | C. | 24或8$\sqrt{5}$ | D. | 8$\sqrt{5}$ |
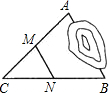 如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=30m,则AB=60m.
如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=30m,则AB=60m.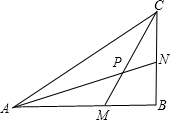 如图,在△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连接AN,CM交于P点,求证:∠APM=45°.
如图,在△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连接AN,CM交于P点,求证:∠APM=45°.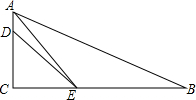 已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE,
已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE,