题目内容
19.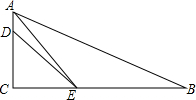 已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE,
已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE,(1)求证:∠B+∠EDA=180°;
(2)求$\frac{AD+AB}{AC}$的值.
分析 (1)过E作AB的垂线,根据角平分线的性质得出EC=EF,再根据HL得出△ECD≌△EFB,从而得出∠EDC=∠B,再根据∠EDC+∠EDA=180°,即可得出答案;
(2)根据(1)证出的全等得出CD=FB,同理得出Rt△EAC≌Rt△EAF,从而得出CA=FA,再根据$\frac{AD+AB}{AC}$=$\frac{AC-CD+AF+FB}{AC}$,即可得出答案.
解答  解:(1)过E作AB的垂线,垂足是F,
解:(1)过E作AB的垂线,垂足是F,
∵AE是角平分线,∠C=90°
∴EC=EF,
又∵EB=ED,
在△ECD和△EFB中,
$\left\{\begin{array}{l}{DE=EB}\\{EC=EF}\end{array}\right.$,
∴△ECD≌△EFB (HL),
∴∠EDC=∠B,
∵∠EDC+∠EDA=180°,
∴∠B+∠EDA=180°;
(2)∵Rt△ECD≌Rt△EFB,
∴CD=FB,
同理Rt△EAC≌Rt△EAF(HL),
∴CA=FA,
∴$\frac{AD+AB}{AC}$=$\frac{AC-CD+AF+FB}{AC}$=$\frac{2AC}{AC}$=2.
点评 此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质、角平分线的性质,关键是根据题意作出辅助线,构造直角三角形.

练习册系列答案
相关题目
7.某市为了解初中学生体能情况,抽取了50名初中毕业的女学生进行“一分钟仰卧起坐”次数测试,测试的情况绘制成表格如下:
(1)求这次抽样测试数据的平均数、众数和中位数;
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少.
| 次数 | 6 | 12 | 15 | 18 | 20 | 25 | 27 | 30 | 32 | 35 | 36 |
| 人数 | 1 | 2 | 8 | 16 | 10 | 5 | 1 | 2 | 1 | 1 | 3 |
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少.
8.有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
| 与标准质量的差值(千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 8 | 2 | 3 | 2 | 4 |
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
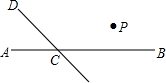 如图,直线CD与直线AB相交于C,根据下列语句画图
如图,直线CD与直线AB相交于C,根据下列语句画图 如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的坐标为(5,$\frac{3}{2}$).
如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的坐标为(5,$\frac{3}{2}$). 对于边长为3的正方形ABCD,建立适当的直角坐标系,写出各个顶点的坐标.
对于边长为3的正方形ABCD,建立适当的直角坐标系,写出各个顶点的坐标. 如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC. 如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:
如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论: