题目内容
2.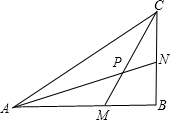 如图,在△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连接AN,CM交于P点,求证:∠APM=45°.
如图,在△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连接AN,CM交于P点,求证:∠APM=45°.
分析 可过点M作ME∥AN,使ME=CN,连NE,AE,得出四边形MENC为平行四边形,再通过求证△AME≌△CBM,可得出△AEN为等腰直角三角形,即可解答.
解答 证明:如图,过M作ME∥AN,使ME=CN,连结NE,AE,
则四边形MENC为平行四边形,
∴∠APM=∠ANE,∠MCN=∠MEN,
∵∠EMB=∠B=90°,
∴∠AME=90°,
由CN=MB,CN=ME,
∴MB=ME,
在△AME和△CBM中,
$\left\{\begin{array}{l}{MB=ME}\\{∠AME=∠CBM=9{0}^{°}}\\{AM=BC}\end{array}\right.$,
∴△AME≌△CBM,
∵AE=MC=EN,
∴∠AEM+∠MEN=∠AEM+∠BCM=∠AEM+∠MAE=90°,
∴△AEN为等腰直角三角形,
∴∠ANE=45°,即∠APM=45°.
点评 本题主要考查平行四边形的判定及性质,等腰直角三角形的性质及全等三角形的判定及性质,解决本题的关键是作出辅助线.

练习册系列答案
相关题目
12.如图中的线段,直线或射线,能相交的是( )
| A. |  | B. |  | C. |  | D. |  |
17.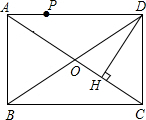 如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )
如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )
 如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )
如图,点P是矩形ABCD所得边AD上的一个动点.DH⊥AC于H,那么点P到矩形的两条对角线AC和BD的距离之和等于( )| A. | 2DH | B. | $\frac{3}{2}DH$ | C. | DH | D. | $\frac{2}{3}DH$ |
7.某市为了解初中学生体能情况,抽取了50名初中毕业的女学生进行“一分钟仰卧起坐”次数测试,测试的情况绘制成表格如下:
(1)求这次抽样测试数据的平均数、众数和中位数;
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少.
| 次数 | 6 | 12 | 15 | 18 | 20 | 25 | 27 | 30 | 32 | 35 | 36 |
| 人数 | 1 | 2 | 8 | 16 | 10 | 5 | 1 | 2 | 1 | 1 | 3 |
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少.
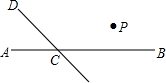 如图,直线CD与直线AB相交于C,根据下列语句画图
如图,直线CD与直线AB相交于C,根据下列语句画图 如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的坐标为(5,$\frac{3}{2}$).
如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的坐标为(5,$\frac{3}{2}$). 如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC. 如图,正六边形ABCDEF的边长为2$\sqrt{3}$,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,
如图,正六边形ABCDEF的边长为2$\sqrt{3}$,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,