题目内容
17.三角形两边长分别是8和6,第三边长是一元二次方程x2-16x+60=0一个实数根,则该三角形的面积是( )| A. | 24 | B. | 48 | C. | 24或8$\sqrt{5}$ | D. | 8$\sqrt{5}$ |
分析 先利用因式分解法解方程得到所以x1=6,x2=10,再分类讨论:当第三边长为6时,如图,在△ABC中,AB=AC=6,BC=8,作AD⊥BC,则BD=CD=4,利用勾股定理计算出AD=2$\sqrt{5}$,接着计算三角形面积公式;当第三边长为10时,利用勾股定理的逆定理可判断此三角形为直角三角形,然后根据三角形面积公式计算三角形面积.
解答 解:x2-16x+60=0
(x-6)(x-10)=0,
x-6=0或x-10=0,
所以x1=6,x2=10,
当第三边长为6时,如图,
在△ABC中,AB=AC=6,BC=8,作AD⊥BC,则BD=CD=4,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
所以该三角形的面积=$\frac{1}{2}$×8×2$\sqrt{5}$=8$\sqrt{5}$;
当第三边长为10时,由于62+82=102,此三角形为直角三角形,
所以该三角形的面积=$\frac{1}{2}$×8×6=24,
即该三角形的面积为24或8$\sqrt{5}$.
故选C.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
相关题目
7.某市为了解初中学生体能情况,抽取了50名初中毕业的女学生进行“一分钟仰卧起坐”次数测试,测试的情况绘制成表格如下:
(1)求这次抽样测试数据的平均数、众数和中位数;
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少.
| 次数 | 6 | 12 | 15 | 18 | 20 | 25 | 27 | 30 | 32 | 35 | 36 |
| 人数 | 1 | 2 | 8 | 16 | 10 | 5 | 1 | 2 | 1 | 1 | 3 |
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少.
8.有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
| 与标准质量的差值(千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 8 | 2 | 3 | 2 | 4 |
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
5.速算
| -11+3=-8 | -39+(-21)=-60 | (-2015)+2014=-1 |
| -3-(-1.2)=-1.8 | (-$\frac{3}{4}$)-(+$\frac{1}{4}$)=-1 | (0.04)×(-0.05)=-0.002 |
| (-$\frac{2}{3}$)×(-1$\frac{1}{2}$)=1 | (-32)÷(-8)=4 | (-2$\frac{1}{12}$)÷1.25=-$1\frac{2}{3}$ |
| (-3)4=81 | (-$\frac{1}{2}$3)=-$\frac{1}{8}$ | -$\frac{{2}^{2}}{7}$=-$\frac{4}{7}$. |
7.下列语句中哪个是命题( )
| A. | 联结A、B两点 | B. | 等角的余角相等吗? | ||
| C. | 对顶角相等 | D. | 代数式$\sqrt{a}$(a≥0)叫二次根式 |
 如图,正六边形ABCDEF的边长为2$\sqrt{3}$,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,
如图,正六边形ABCDEF的边长为2$\sqrt{3}$,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,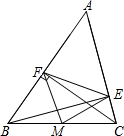 如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,连接MF、ME.
如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,连接MF、ME. 如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论:
如图,点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点(其中P、Q不与端点重合),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论: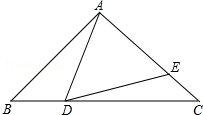 如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.
如图,在△ABC中,AB=AC=10,BC=16,点D是边BC上一动点(不与B,C重合),∠ADE=∠B,DE交AC于点E.