题目内容
6.已知x,y为整数,且满足($\frac{1}{x}$+$\frac{1}{y}$)($\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$)=-$\frac{2}{3}$($\frac{1}{{x}^{4}}$-$\frac{1}{{y}^{4}}$),求x+y的值.分析 根据平方差公式和约分法则把原式化简,根据取整法则解答即可.
解答 解:∵($\frac{1}{x}$+$\frac{1}{y}$)($\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$)=-$\frac{2}{3}$($\frac{1}{{x}^{4}}$-$\frac{1}{{y}^{4}}$),
∴($\frac{1}{x}$+$\frac{1}{y}$)($\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$)=-$\frac{2}{3}$($\frac{1}{{x}^{2}}+\frac{1}{{y}^{2}}$)($\frac{1}{{x}^{2}}$-$\frac{1}{{y}^{2}}$),
∴($\frac{1}{x}$+$\frac{1}{y}$)=-$\frac{2}{3}$($\frac{1}{{x}^{2}}$-$\frac{1}{{y}^{2}}$),
∴($\frac{1}{x}$+$\frac{1}{y}$)[1+$\frac{2}{3}$($\frac{1}{x}$-$\frac{1}{y}$)]=0,
∴$\frac{1}{x}$+$\frac{1}{y}$=0或1+$\frac{2}{3}$($\frac{1}{x}$-$\frac{1}{y}$)=0,
∴x+y=0或$\frac{1}{x}$-$\frac{1}{y}$=-$\frac{3}{2}$,
由$\frac{1}{x}$-$\frac{1}{y}$=-$\frac{3}{2}$得,x=$\frac{2y}{2-3y}$,
整理得,x+y=$\frac{2}{\frac{2}{y}-3}$+y,
当y=1或2时,x为整数-2或-1,
则x+y=±1,
∴x+y的值为0或±1.
点评 本题考查的是分式的混合运算,掌握平方差公式是解题的关键.

| A. | 2013 | B. | 2014 | C. | 2016 | D. | 2017 |
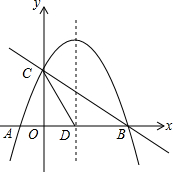 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(-1,0),C(0,2).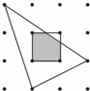 如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为$\frac{11}{12}$.
如图,平面内有16个格点,每个格点小正方形的边长为1,则图中阴影部分的面积为$\frac{11}{12}$. 四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$.
四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$.
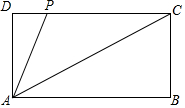 如图,在矩形ABCD中,AB=2,BC=1,P在DC上,当AP=$\frac{\sqrt{5}}{2}$时,△ADP∽△ABC.
如图,在矩形ABCD中,AB=2,BC=1,P在DC上,当AP=$\frac{\sqrt{5}}{2}$时,△ADP∽△ABC.