题目内容
已知x、y是实数，并且
+y2-6y+9=0，则（xy）2014的值是 ．
| 3x+1 |
考点：配方法的应用,非负数的性质：偶次方,非负数的性质：算术平方根
专题：
分析：首先利用配方法由
+y2-6y+9=0，得出
+（y-3）2=0，利用非负数的性质求得x、y的数值，进一步代入求得答案即可．
| 3x+1 |
| 3x+1 |
解答：解：∵
+y2-6y+9=0，
∴
+（y-3）2=0，
∴3x+1=0，y-3=0，
∴x=-
，y=3，
∴（xy）2014=1．
故答案为：1．
| 3x+1 |
∴
| 3x+1 |
∴3x+1=0，y-3=0，
∴x=-
| 1 |
| 3 |
∴（xy）2014=1．
故答案为：1．
点评：此题考查配方法的运用，非负数的性质，掌握二次根式的性质和完全平方公式是解决问题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如图，已知每个小正方形的边长为1cm，O、A、B都在小正方形顶点上，扇形OAB是某个圆锥的侧面展开图．这个圆锥的底面半径郑州市某一日的用水量为82.3452万立方米，比5年来日用水最高记录高出6万多立方米.82.3452万立方米用科学记数法表示为（ ）立方米（保留三个有效数字）
| A、82.3×104 |
| B、8.23×105 |
| C、8.23×104 |
| D、0.823×106 |
如图所示，已知△ABC是等边三角形，D、E分别是AC、BC上的点，∠BDE=60°．
如图，在△ABC中，AB=AC，AD是△ABC的角平分线，若BC=10，AD=12，则AC=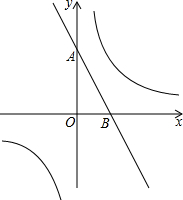
直线y=-2x+2与坐标轴交于A、B两点，在反比例函数y=