题目内容
 如图,BD是⊙O的直径,∠A=62°,则sin∠CBD的值( )
如图,BD是⊙O的直径,∠A=62°,则sin∠CBD的值( )A、大于
| ||
B、等于
| ||
C、小于
| ||
| D、二者不可比较 |
考点:圆周角定理,锐角三角函数的增减性,互余两角三角函数的关系
专题:
分析:首先连接CD,由在同圆或等圆中,同弧或等弧所对的圆周角相等,可得∠D=∠A=62°,又由BD是⊙O的直径,根据半圆(或直径)所对的圆周角是直角,即可得∠BCD=90°,继而求得∠CBD的度数,根据正弦函数的增减性,即可求得答案.
解答: 解:连接CD,
解:连接CD,
∵∠A与∠D是
对的圆周角,
∴∠D=∠A=62°,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠CBD=90°-∠D=28°<30°,
∵sin30°=
,
∴sin∠CBD<
.
故选C.
 解:连接CD,
解:连接CD,∵∠A与∠D是
 |
| BC |
∴∠D=∠A=62°,
∵BD是⊙O的直径,
∴∠BCD=90°,
∴∠CBD=90°-∠D=28°<30°,
∵sin30°=
| 1 |
| 2 |
∴sin∠CBD<
| 1 |
| 2 |
故选C.
点评:此题考查了圆周角定理与三角函数的增减性问题.此题难度适中,解题的关键是准确作出辅助线,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等与半圆(或直径)所对的圆周角是直角定理的应用.

练习册系列答案
相关题目

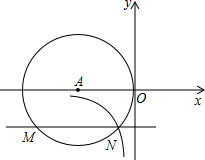 如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙O于M、N两点,若点M的坐标是(-4,-2),过点N的双曲线是
如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙O于M、N两点,若点M的坐标是(-4,-2),过点N的双曲线是