题目内容
现有若干个完全相同的硬币(硬币的正、反面图案不同),按如下方式抛掷硬币:
方式一:从中选取一枚硬币抛掷;
方式二:从中选取两枚硬币抛掷;
方式三:从中选取三枚硬币抛掷.
请你在每一种抛掷方式中,各找出一种随机现象,使得这三种随机现象的概率相等(要求:概率不能为0或1),并说明理由.
方式一:从中选取一枚硬币抛掷;
方式二:从中选取两枚硬币抛掷;
方式三:从中选取三枚硬币抛掷.
请你在每一种抛掷方式中,各找出一种随机现象,使得这三种随机现象的概率相等(要求:概率不能为0或1),并说明理由.
考点:列表法与树状图法
专题:
分析:根据三种方式分别得出方式一:出现正面向上的概率与方式二:出现一正一反的概率和方式三:出现两个反面以上的概率,即可得出答案.
解答: 解:方式一:从中选取一枚硬币抛掷;出现正面向上的概率为:
解:方式一:从中选取一枚硬币抛掷;出现正面向上的概率为:
,
方式二:从中选取两枚硬币抛掷,可能出现的情况为:正正,反反,正反,反正,
出现一正一反的概率为:
,
方式三:从中选取三枚硬币抛掷,出现两个反面以上的概率为:
.
故方式一:出现正面向上的概率与方式二:出现一正一反的概率和方式三:出现两个反面以上的概率相等.
 解:方式一:从中选取一枚硬币抛掷;出现正面向上的概率为:
解:方式一:从中选取一枚硬币抛掷;出现正面向上的概率为:| 1 |
| 2 |
方式二:从中选取两枚硬币抛掷,可能出现的情况为:正正,反反,正反,反正,
出现一正一反的概率为:
| 1 |
| 2 |
方式三:从中选取三枚硬币抛掷,出现两个反面以上的概率为:
| 1 |
| 2 |
故方式一:出现正面向上的概率与方式二:出现一正一反的概率和方式三:出现两个反面以上的概率相等.
点评:此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
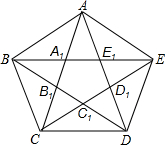 如图,在正五边形ABCDE中,对角线分别相交于点A1、B1、C1、D1、E1.将所有全等的三角形视为一类,称为一个“全等类”( 如△ABC、△BCD与△CDE等都属于同一个全等类).则图中不同全等类的个数为( )
如图,在正五边形ABCDE中,对角线分别相交于点A1、B1、C1、D1、E1.将所有全等的三角形视为一类,称为一个“全等类”( 如△ABC、△BCD与△CDE等都属于同一个全等类).则图中不同全等类的个数为( )| A、3 | B、4 | C、5 | D、6 |
 如图,BD是⊙O的直径,∠A=62°,则sin∠CBD的值( )
如图,BD是⊙O的直径,∠A=62°,则sin∠CBD的值( )A、大于
| ||
B、等于
| ||
C、小于
| ||
| D、二者不可比较 |
 如图,在梯形ABCD中,AD∥BC,AB=DC,点O为底边AD的中点.求证:OB=OC (要求:写出证明过程中的重要依据)
如图,在梯形ABCD中,AD∥BC,AB=DC,点O为底边AD的中点.求证:OB=OC (要求:写出证明过程中的重要依据) ,则该汽车的车牌号码是
,则该汽车的车牌号码是