题目内容
19．在等腰△ABC中，一腰AB的垂直平分线交另一腰AC于点G，若已知AB=10，△GBC的周长为17，则底BC的长为（ ）| A． | 10 | B． | 9 | C． | 7 | D． | 5 |
分析 首先根据题意画出图形，然后由在等腰△ABC中，一腰AB的垂直平分线交另一腰AC于点G，根据线段垂直平分线的性质，可得AG=BG，继而可得△GBC的周长=AC+BC=17，则可求得答案．
解答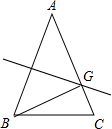 
解：如图，∵在等腰△ABC中，一腰AB的垂直平分线交另一腰AC于点G，
∴AG=BG，
∵AB=10，△GBC的周长为17，
∴CG+BG+BC=CG+AG+BC=AC+BC=17，AC=AB=10，
∴BC=7．
故选C．
点评 本题主要考查线段垂直平分线的性质，掌握线段垂直平分线的点到线段两端点的距离相等是解题的关键．
练习册系列答案
相关题目
9．近年来，我国持续大面积的雾霾天气让环保和健康问题成为全社会关注的焦点．为进一步普及环保和健康知识，某初中学校进行了“关注环境•保护环境”的知识竞赛，参加决赛的15名选手的成绩统计见下表，则参加决赛的选手的成绩的众数和中位数是（ ）
| 成绩 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 3 | 4 | 5 | 2 | 1 |
| A． | 70分，80分 | B． | 70分，70分 | C． | 80分，80分 | D． | 80分，90分 |
10．下列方程中有解的是（ ）
| A． | x2+x-1=0 | B． | x2+x+1=0 | C． | |x|=-1 | D． | $\frac{x-1}{x+2}$=$\frac{x-3}{2+x}$ |
14．计算a2•a4÷（-a2）2的结果是（ ）
| A． | a | B． | a2 | C． | -a2 | D． | a3 |
如图是每个面都标注了字母的立方体的表面展开图．在展开前，与标注字母c的面相对的面上的字母为（ ）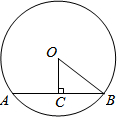
如图，AB是⊙O的弦，OC⊥AB，垂足为C．若AB=2，OC=$\sqrt{3}$，则∠COB的值为30°．?
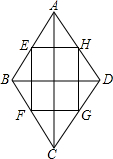如图，E、F、G、H分别是菱形ABCD四边的中点，菱形ABCD的面积为4$\sqrt{3}$cm2，对角线AC=2$\sqrt{2}$cm．