题目内容
8.已知x1,x2是关于x的方程x2+m2x+n=0的两个实根,y1、y2是关于y的方程y2+5my+7=0的两个实数根,且x1-y1=2,x2-y2=2,则m=4,n=-29.分析 由根与系数的关系可得:x1+x2=-m2,y1+y2=-5m,y1•y2=7与x1-y1=x2-y2=2联立可解出m、n的值.
解答 解:根据题意得x1+x2=-m2,y1+y2=-5m,
两式相减得x1-y1+x2-y2=-m2+5m,
所以2+2=-m2+5m,
整理得m2-5m+4=0,解得m1=1,m2=4,
当m=1时,方程x2+x+1=0和方程y2+5y+7=0都没有实数根,
所以m的值为4.
因此y1+y2=-20,联立y1•y2=7,解得y1=-10+$\sqrt{93}$,y2=-10-$\sqrt{93}$.
又x1-y1=x2-y2=2
解得x1=-8+$\sqrt{93}$,x2=-8-$\sqrt{93}$,
又x1•x2=n
解得:n=-29
m=4,n=-29.
故答案为:4,-29.
点评 本题考查了根与系数的关系的知识,解答本题要掌握若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列说法中,错误的是( )
| A. | 全等三角形对应角相等 | B. | 全等三角形对应边相等 | ||
| C. | 全等三角形的面积相等 | D. | 面积相等的两个三角形一定全等 |
 如图,A,B两点分别位于一个池塘的两端,小聪明用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为14m,则A,B间的距离为28m.
如图,A,B两点分别位于一个池塘的两端,小聪明用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为14m,则A,B间的距离为28m.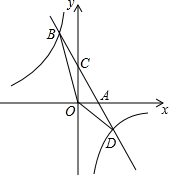 如图,在平面直角坐标系中,直线AB与x轴交于点A(1,0),与反比例函数在第二象限内的图象交于B(-1,n),连接BO,若S△AOB=2.
如图,在平面直角坐标系中,直线AB与x轴交于点A(1,0),与反比例函数在第二象限内的图象交于B(-1,n),连接BO,若S△AOB=2.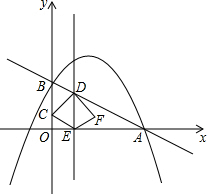 如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,抛物线y=-$\frac{1}{2}$x2+bx+c经过A,B两点.
如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点A,与y轴交于点B,抛物线y=-$\frac{1}{2}$x2+bx+c经过A,B两点.