题目内容
10.在△ABC中,三条边分别为a,b,c,下列各式中,能成立的个数是( )①∠A:∠B:∠C=1:2:3
②a:b:c=3:4:7
③∠A:∠B:∠C=3:4:5
④a:b:c=32:42:72.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①∠A:∠B:∠C=1:2:3,根据三角形内角和定理可求:∠A=30°,∠B=60°,∠C=90°,可判断△ABC为直角三角形;
②a:b:c=3:4:7,由3+4=7,根据三角形三边关系,可判断不能组成三角形;
③∠A:∠B:∠C=3:4:5,根据三角形内角和定理可求:∠A=45°,∠B=60°,∠C=105°,可判断△ABC为钝角三角形;
④a:b:c=32:42:72,由32+42<72,据三角形三边关系,可判断不能组成三角形.综合以上信息可得能成立的个数.
解答 解:①∵∠A:∠B:∠C=1:2:3,且∠A+∠B+∠C=180°,
∴∠A=30°,∠B=60°,∠C=90°,
∴△ABC为直角三角形,故能成立;
②∵a:b:c=3:4:7,且3+4=7,
∴不能组成三角形,故不成立;
③∵∠A:∠B:∠C=3:4:5,且∠A+∠B+∠C=180°,
∴∠A=45°,∠B=60°,∠C=105°,
∴△ABC为钝角三角形,故能成立;
④∵a:b:c=32:42:72,且32+42<72,
∴不能组成三角形,故不成立.
∴能成立的是①③,
故选:B.
点评 此题考查了本题考查了三角形的三边关系,判断三条线段是否能组成三角形主要是根据三角形的任意两边之和大于第三边.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
5.若a=$\frac{1}{b}$-$\frac{1}{c}$,则c=( )
| A. | $\frac{1+ab}{b}$ | B. | b-$\frac{1}{a}$ | C. | b+$\frac{1}{a}$ | D. | $\frac{b}{1-ab}$ |
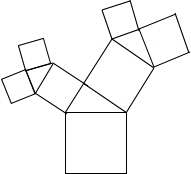 如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2.
如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则所有正方形的面积的和是( )cm2.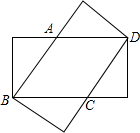 如图,四边形EBGD和四边形BFDH是两个全等的矩形,其中ED、BH交于点A,BG、FD交于点C.
如图,四边形EBGD和四边形BFDH是两个全等的矩形,其中ED、BH交于点A,BG、FD交于点C.