题目内容
4.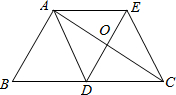 如图,在△ABC中,AD是△ABC的中线,过点A作AE∥BC与AB的平行线DE交于点E,DE与AC相交于点O,连接EC.
如图,在△ABC中,AD是△ABC的中线,过点A作AE∥BC与AB的平行线DE交于点E,DE与AC相交于点O,连接EC.(1)求证:AD∥EC;
(2)当△ABC满足条件∠BAC=90°时,四边形ADCE是菱形,请补充条件并证明.
分析 (1)根据两组对边分别平行的四边形是平行四边形可得四边形ABDE是平行四边形,进而可得AE=DB,再根据一组对边平行且相等的四边形是平行四边形可得四边形ADCE是平行四边形,进而可得AD∥EC;
(2)添加∠BAC=90°,根据直角三角形斜边的中线等于斜边的一半可得AD=$\frac{1}{2}$BC,然后证明AD=CD可得四边形ADCE是菱形.
解答 证明:(1)∵AE∥BC,AB∥DE,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵AD是△ABC的中线,
∴BD=CD,
∴AE=DC,
∵AE∥BC,
∴四边形ADCE是平行四边形,
∴AD∥EC;
(2)添加∠BAC=90°,
∵AD是△ABC的中线,
∴AD=DC=$\frac{1}{2}$BC,
∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形.
点评 此题主要考查了菱形的判定,以及平行四边形的判定和性质,关键是掌握一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
 如图,△ABC中,∠ACB=90°,∠1=∠A.
如图,△ABC中,∠ACB=90°,∠1=∠A.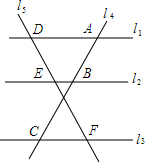 如图,两条直线被三条平行线所截,且$\frac{DE}{EF}$=$\frac{2}{3}$,AB=6,求AC的长.
如图,两条直线被三条平行线所截,且$\frac{DE}{EF}$=$\frac{2}{3}$,AB=6,求AC的长.