题目内容
18. 某农场要建一个长方形的养鸡场,鸡场的一边靠墙,(墙长25m)另外三边用木栏围成,木栏长40m
某农场要建一个长方形的养鸡场,鸡场的一边靠墙,(墙长25m)另外三边用木栏围成,木栏长40m(1)若养鸡场面积为150m2,求鸡场两边的长分别是多少?
(2)养鸡场面积有最大值吗?如果有,求养鸡场的最大面积;如果没有,请说明理由.
分析 (1)首先设出鸡场宽为x米,则长(40-2x)米,然后根据矩形的面积=长×宽,用未知数表示出鸡场的面积,根据面积为200m2,可得方程,解方程即可;
(2)直接利用配方法求出二次函数最值即可.
解答 解:(1)设宽为x米,长(40-2x)米,根据题意得:
x(40-2x)=150,
-2x2+40x-150=0,
解得:x1=15,x2=5(不合题意,舍去),
则鸡场靠墙的一边长为:40-2x=10.
答:鸡场两边的长分别是15m,10m.
(2)养鸡场面积有最大值,
设总面积为y,则y=x(40-2x)=-2x2+40x=-2(x-10)2+200,
∴当x=10米时,y最大=200平方米.
点评 此题主要考查了一元二次方程的应用以及二次函数最值求法等知识,读懂题意,找到等量关系准确的列出方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13. 如图所示,△ABC绕点A旋转至△AEF,其旋转角是( )
如图所示,△ABC绕点A旋转至△AEF,其旋转角是( )
 如图所示,△ABC绕点A旋转至△AEF,其旋转角是( )
如图所示,△ABC绕点A旋转至△AEF,其旋转角是( )| A. | ∠BAE | B. | ∠CAE | C. | ∠EAF | D. | ∠BAF |
7.已知a、b互为相反数,且a-2b=3,则a的值是( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
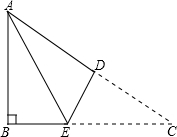 如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于多少cm?
如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于多少cm?