题目内容
10．
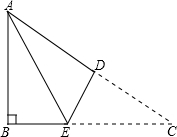如图，Rt△ABC中，∠B=90°，AB=3cm，AC=5cm，将△ABC折叠，使点C与A重合，得折痕DE，则△ABE的周长等于多少cm？
分析 根据勾股定理，可得BC的长，根据翻折的性质，可得AE与CE的关系，根据三角形的周长公式，可得答案．
解答 解：在Rt△ABC中，∠B=90°，AB=3cm，AC=5cm，
由勾股定理，得
BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=4．
由翻折的性质，得
CE=AE．
△ABE的周长=AB+BE+AE=AB+BE+CE=AB+BC=3+4=7cm．
答：△ABE的周长等于7cm．
点评 本题考查了翻折的性质，利用了勾股定理，利用翻折的性质得出CE与AE的关系是解题关键，又利用了等量代换．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
相关题目
1．已知a＞1，下列各式正确的是（ ）
| A． | $\sqrt{\frac{1}{a}}$＞a | B． | $\frac{1}{{\sqrt{a}}}$＞（$\sqrt{a}$）2 | C． | $\frac{1}{{\sqrt{a}}}$＜$\frac{1}{a}$ | D． | a＞$\sqrt{a}$ |
某农场要建一个长方形的养鸡场，鸡场的一边靠墙，（墙长25m）另外三边用木栏围成，木栏长40m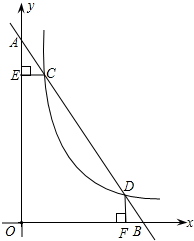
在平面直角坐标系中，已知直线AB 与y轴交于点A，与x轴交于点B，与双曲线y=$\frac{m}{x}$（x＞0）交于点C（1，6）和点D（3，n）．作CE⊥y轴于E，DF⊥x轴于F．