题目内容
8.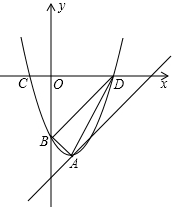 如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.
如图,抛物线y=x2-2x+c的顶点A在直线l:y=x-5上.(1)求抛物线顶点A的坐标;
(2)设抛物线与y轴交于点B,与x轴交于点C、D(C点在D点的左侧),试判断△ABD的形状;
(3)求出点C到直线BD的距离.
分析 (1)先根据抛物线的解析式得出其对称轴,由此得到顶点A的横坐标,然后代入直线l的解析式中求出点A的纵坐标即可,
(2)先由抛物线的解析式得到点B的坐标,再求出AB、AD、BD三边的长,然后根据勾股定理的逆定理即可确定△ABD是直角三角形;
(3)连接BC,过点C作CE⊥BD,易求△BCD的面积,由(2)可知BD的长,进而可求出CE的长,即点C到直线BD的距离.
解答 解:(1)∵y=x2-2x+c,
∴顶点A的横坐标为x=-$\frac{-2}{2}$=1,
又∵顶点A在直线y=x-5上,
∴当x=1时,y=1-5=-4,
∴点A的坐标为(1,-4);
(2)△ABD是直角三角形.理由如下:
∵抛物线y=x2-2x-3与y轴交于点B,
∴B(0,-3).
当y=0时,x2-2x-3=0,
解得x1=-1,x2=3,
∴C(-1,0),D(3,0).
∵BD2=OB2+OD2=18,AB2=(4-3)2+12=2,AD2=(3-1)2+42=20,
∴BD2+AB2=AD2,
∴∠ABD=90°,
即△ABD是直角三角形;
(3)连接BC,过点C作CE⊥BD,
∵OC=1,OD=3,
∴CD=4,
∵OB=3,
∴S△BCD=$\frac{1}{2}$CD•OB=6,
∵BD=$\sqrt{18}$=3$\sqrt{2}$,
∵$\frac{CE•BD}{2}$=6,
∴CE=$\frac{12}{BD}=\frac{12}{3\sqrt{2}}$=2$\sqrt{2}$,
即点C到直线BD的距离是2$\sqrt{2}$.
点评 本题考查了二次函数的性质、运用待定系数法确定其解析式、勾股定理及其逆定理以及三角形面积公式的运用等知识,综合性较强,难度适中,正确做出C到直线BD的垂线段是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
18.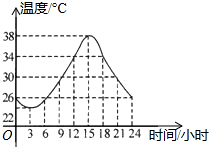 如图是某市一天的温度随时间变化的图象,通过观察可知下列说法错误的是( )
如图是某市一天的温度随时间变化的图象,通过观察可知下列说法错误的是( )
 如图是某市一天的温度随时间变化的图象,通过观察可知下列说法错误的是( )
如图是某市一天的温度随时间变化的图象,通过观察可知下列说法错误的是( )| A. | 这天15点时温度最高 | |
| B. | 这天3点时温度最低 | |
| C. | 这天最高温度与最低温度的差是16℃ | |
| D. | 这天1点时温度是30℃ |
19.多项式2a2b-πab2-ab的项数及次数分别为( )
| A. | 3,4 | B. | 3,3 | C. | 3,2 | D. | 2,3 |
3.数学兴趣小组的甲、乙、丙、丁四位同学进行还原魔方练习,下表记录了他们10次还原魔方所用时间的平均值$\overline{x}$与方差S2:
要从中选择一名还原魔方用时少又发挥稳定的同学参加比赛,应该选择( )
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$(秒) | 30 | 30 | 28 | 28 |
| S2 | 1.21 | 1.05 | 1.21 | 1.05 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
17. 如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )
如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )
 如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )
如图,2×3的网格是由边长为a的小正方形组成,那么图中阴影部分的面积是( )| A. | a2 | B. | $\frac{3}{2}$a2 | C. | 2a2 | D. | 3a2 |
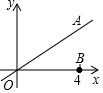 如图,直线OA是一次函数y=$\frac{x}{2}$的图象,点B的坐标是(4,0),点C在直线OA上且△OBC为等腰三角形,满足条件的C点共有4个.
如图,直线OA是一次函数y=$\frac{x}{2}$的图象,点B的坐标是(4,0),点C在直线OA上且△OBC为等腰三角形,满足条件的C点共有4个.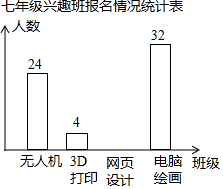 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.
学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.