题目内容
5. 如图,正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BC,EH⊥AE,MN⊥BD,求证:EN=$\frac{1}{2}$BD.
如图,正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BC,EH⊥AE,MN⊥BD,求证:EN=$\frac{1}{2}$BD.
分析 如图,连接AC交BD于O.,作EK⊥AB于K.由△AEK≌△MEF,推出AE=EM,由△AOE≌△ENM,推出EN=OA,由此即可解决问题.
解答 证明:如图,连接AC交BD于O.,作EK⊥AB于K.
∵四边形ABCD是正方形,
∴AC⊥BD,∠ABD=∠CBD=45°,OA=OC=OB=OD,
∵EK⊥AB,EF⊥BC,
∴EK=EF,
∵∠EKB=∠KBF=∠BFE=90°,
∴四边形EKBF是矩形,
∴∠KEF=∠AEM=90°,
∴∠AEK=∠MEF,∵∠EKA=∠EFM=90°,
∴△AEK≌△MEF,
∴AE=EM,
∵○EAO+∠AEO=90°,∠AEO+∠MEN=90°,
∴○EAO=∠MEN,∵∠AOE=∠MNE=90°,
∴△AOE≌△ENM,
∴EN=OA,
∵OA=$\frac{1}{2}$BD,
∴EN=$\frac{1}{2}$BD.
点评 本题考查正方形的性质、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.下列计算中,正确的是( )
| A. | a2+a3=a5 | B. | a2•a3=a6 | C. | a9÷a3=a3 | D. | (-a3)2=a6 |
16.下列事件为必然事件的有( )个
①过三点可以确定一个圆 ②平分弦的直径必垂直这条弦
③一个数的零次幂为零 ④两点确定一条直线.
①过三点可以确定一个圆 ②平分弦的直径必垂直这条弦
③一个数的零次幂为零 ④两点确定一条直线.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
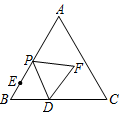 如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是8.
如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是8.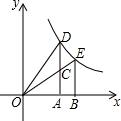 如图,在平面直角坐标系中,点D的函数y=$\frac{k}{x}$(x>0)的图象上,DA垂直x轴于点A,点C为线段AD的中心,延长线段OC交函数y=$\frac{k}{x}$(x>0)的图象于点E,EB垂直x轴于点B,若直角梯形ABEC的面积为1,则k的值为4.
如图,在平面直角坐标系中,点D的函数y=$\frac{k}{x}$(x>0)的图象上,DA垂直x轴于点A,点C为线段AD的中心,延长线段OC交函数y=$\frac{k}{x}$(x>0)的图象于点E,EB垂直x轴于点B,若直角梯形ABEC的面积为1,则k的值为4. 如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,与对角线BD相交于点H.若BD=BF,求BE的长.
如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G,与对角线BD相交于点H.若BD=BF,求BE的长.