题目内容
18.如图,在△ABC中,∠ACB=90°,AC=BC,D为BC上一动点,CE⊥AD于P,交AB于点E,(3)若AC=2,O为AB中点,连接PO,如图3,求∠APO的度数.(1)若AD平分∠BAC,如图1,求证:BE=CD;
(2)若D为BC的中点,如图2,求证:AE=2BE;
(3)若AC=2,O为AB中点,连接PO,如图3,求∠APO的度数.
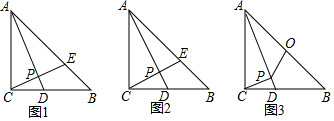
分析 (1)如图1,作辅助线,构建△ACD≌△CBG,再证明BE=BG可得结论;
(2)如图2,证明△AEC∽△BEG,根据对应边的比:$\frac{AE}{EB}=\frac{AC}{BG}=2$,可得结论;
(3)如图3,作辅助线,构建全等三角形和等腰直角三角形,证明CP=BF,所以Rt△CDP≌Rt△BGF,得∠PCD=∠FBG,再证明△OCP≌△OBF,可以得△POF是等腰直角三角形,可得∠APO=90°-45°=45°.
解答  证明:(1)如图1,过B作BG⊥BC,交CE的延长线于G,
证明:(1)如图1,过B作BG⊥BC,交CE的延长线于G,
∵∠ACB=90°,
∴∠ACP+∠PCD=90°,
∵AD⊥CE,
∴∠APC=90°,
∴∠ACP+∠CAD=90°,
∴∠PCD=∠CAD,
∵∠ACD=∠CBG=90°,
AC=BC,
∴△ACD≌△CBG(ASA),
∴CD=BG,
∵∠CBG=90°,∠ABC=45°,
∴∠EBG=45°,
∵∠BEG=∠AEC=90°-$\frac{45°}{2}$=67.5°,
∴∠G=180°-45°-67.5°=67.5°,
∴∠G=∠BEG,
∴BE=BG,
∴CD=BE;
(2)如图2,过B作BG⊥BC,交CE的延长线于G,
同(1)得:△ACD≌△CBG,
∴CD=BG,
∵D是BC的中点,
∴CD=BG=$\frac{1}{2}$BC=$\frac{1}{2}$AC,
∵BG∥AC,
∴△AEC∽△BEG,
∴$\frac{AE}{EB}=\frac{AC}{BG}=2$,
∴AE=2BE,
(3)如图3,过B作BG⊥BC,交CE的延长线于G,过B作BF⊥CE于F,连接OC、OF,
易证明△ACD≌△CBG,
∴CD=BG,∠ADC=∠G,AD=CG,
∵S△ACD=S△CBG,
∴$\frac{1}{2}$AD•CP=$\frac{1}{2}$CG•BF,
∴CP=BF,
∴Rt△CDP≌Rt△BGF(HL),
∴∠PCD=∠FBG,
在Rt△ACB中,O是AB的中点,
∴CO=BO,
∵∠OCP=90°-∠ACO-∠PCD,
∠OBF=90°-∠ABC-∠FBG,
∵∠ACO=∠ABC=45°,
∴∠OCP=∠OBF,
∴△OCP≌△OBF,
∴OP=OF,∠COP=∠BOF,
∴∠POF=90°,
∴△POF是等腰直角三角形,
∴∠OPF=45°,
∵∠APE=90°,
∴∠APO=90°-45°=45°.
点评 本题是三角形的综合题,考查了全等三角形的性质和判定、等腰直角三角形的性质、相似三角形的性质和判定,本题能证明△ACD≌△CBG是关键,第二问利用三角形相似得出AE和BE的关系,第三问根据直角三角形斜边上的中线等于斜边的一半,再构建一对三角形全等,使问题得以解决.

| A. | $\frac{8}{x}$-$\frac{8}{2x}$=$\frac{1}{3}$ | B. | $\frac{8}{x}$$-\frac{8}{2x}$=20 | C. | $\frac{8}{2x}$-$\frac{8}{x}$=$\frac{1}{3}$ | D. | $\frac{8}{2x}$$-\frac{8}{x}$=20 |
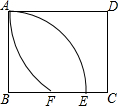 如图,矩形ABCD中,AB=12,BC=13,以B为圆心,BA为半径画弧,交BC于点E,以D为圆心,DA为半径画弧,交BC于点F,则EF的长为( )
如图,矩形ABCD中,AB=12,BC=13,以B为圆心,BA为半径画弧,交BC于点E,以D为圆心,DA为半径画弧,交BC于点F,则EF的长为( )| A. | 3 | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
| A. | (a-2)2=a2-4 | B. | a2•a4=a8 | C. | a3+a2=2a5 | D. | (-ab2)3=-a3b6 |
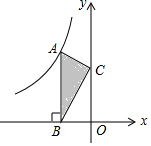 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为4,则k的值是( )| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
| A. | a2•a3 | B. | a4+a2 | C. | a12÷a2 | D. | (a3)2 |
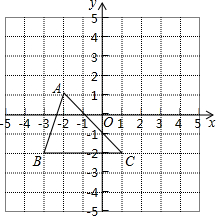 如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′. 如图,在?ABCD中,E,F分别在边AD,BC上,且AE=CF,连接EF,请你只用无刻度的直尺画出线段EF的中点O,并说明这样画的理由.
如图,在?ABCD中,E,F分别在边AD,BC上,且AE=CF,连接EF,请你只用无刻度的直尺画出线段EF的中点O,并说明这样画的理由.