题目内容
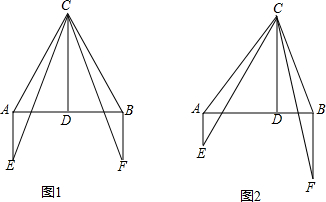
如图,C为线段AB上一动点,过A作AD⊥AB且AD=3,过B作BE⊥AB且BE=1,连接DC、EC,若AB=5,设AC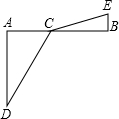 =x.
=x.(1)DC+EC的长为
(2)当点C的位置满足
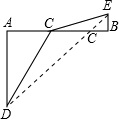
(3)根据以上结论,你能通过构图求出
| x2+4 |
| (4-x)2+25 |
分析:(1)表示出BC的长度,然后分别在Rt△ACD与Rt△BCE中利用勾股定理求出DC与EC的长度,相加即可;
(2)根据两点之间线段最短,当点C、D、E在同一直线时,DC+EC的长最小,此时△ACD与△BCE相似,根据相似三角形对应边成比例列式即可求出x的值,再代入进行计算即可求解;
(3)根据(2)的求解思路画出示意图并利用相似三角形对应边成比例列式求解即可.
(2)根据两点之间线段最短,当点C、D、E在同一直线时,DC+EC的长最小,此时△ACD与△BCE相似,根据相似三角形对应边成比例列式即可求出x的值,再代入进行计算即可求解;
(3)根据(2)的求解思路画出示意图并利用相似三角形对应边成比例列式求解即可.
解答:解:(1)∵AB=5,AC=x,
∴BC=5-x,
∵AD=3,BE=1,
∴DC=
=
,
EC=
=
,
∴DC+EC的长为:
+
;
(2)如图,根据两点之间线段最短可知,当点C、D、E在同一直线时,DC+EC的长最小,
 此时,∠ACD=∠BCE(对顶角相等),
此时,∠ACD=∠BCE(对顶角相等),
∠A=∠B=90°(垂直定义),
∴△ACD∽△BCE,
∴
=
,
即
=
,
解得x=
,
此时,DC+EC=
+
=
+
=
;
(3)如图所示,
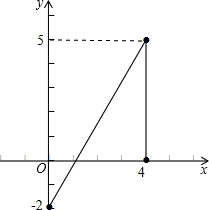 根据(2)中的求解思路,
根据(2)中的求解思路,
当
=
时,
即x=
时,
+
有最小值,
此时
+
=
=
.
∴BC=5-x,
∵AD=3,BE=1,
∴DC=
| AD2+AC2 |
| 32+x2 |
EC=
| BE2+EC2 |
| 12+(5-x)2 |
∴DC+EC的长为:
| 32+x2 |
| 12+(5-x)2 |
(2)如图,根据两点之间线段最短可知,当点C、D、E在同一直线时,DC+EC的长最小,
 此时,∠ACD=∠BCE(对顶角相等),
此时,∠ACD=∠BCE(对顶角相等),∠A=∠B=90°(垂直定义),
∴△ACD∽△BCE,
∴
| AD |
| BE |
| AC |
| BC |
即
| 3 |
| 1 |
| x |
| 5-x |
解得x=
| 15 |
| 4 |
此时,DC+EC=
| 32+x2 |
| 12+(5-x)2 |
32+(
|
1+(5-
|
| 41 |
(3)如图所示,
 根据(2)中的求解思路,
根据(2)中的求解思路,当
| 2 |
| 5 |
| x |
| 4-x |
即x=
| 8 |
| 7 |
| x2+4 |
| (4-x)2+25 |
此时
| x2+4 |
| (4-x)2+25 |
| (5+2)2+42 |
| 65 |
点评:本题考查了利用轴对称求最短路线的问题,根据两点之间线段最短的性质以及相似三角形对应边成比例列式是解题的关键.

练习册系列答案
相关题目
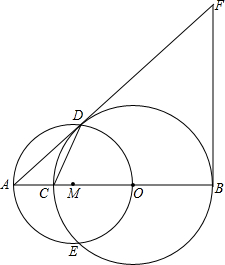 如图,C为线段AB上一点,以BC为直径作⊙O,再以AO为直径作⊙M交⊙O于D、B作AB的垂线交AD的延长线于F,连接CD.若AC=2,且AC与AD的长是关于x的方程x2-
如图,C为线段AB上一点,以BC为直径作⊙O,再以AO为直径作⊙M交⊙O于D、B作AB的垂线交AD的延长线于F,连接CD.若AC=2,且AC与AD的长是关于x的方程x2- 如图,C为线段AB上的一点,△ACM、△CBN都是等边三角形,若AC=3,BC=2,则△MCD与△BND的面积比为
如图,C为线段AB上的一点,△ACM、△CBN都是等边三角形,若AC=3,BC=2,则△MCD与△BND的面积比为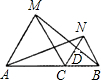 如图,C为线段AB上的一点,△ACM、△CBN都是等边三角形,BM与CN交于D点.若AC=3,BC=2,则CD=
如图,C为线段AB上的一点,△ACM、△CBN都是等边三角形,BM与CN交于D点.若AC=3,BC=2,则CD= 7、如图,P为线段AB上一点,AD与BC交干E,∠CPD=∠A=∠B,BC交PD于E,AD交PC于G,则图中
7、如图,P为线段AB上一点,AD与BC交干E,∠CPD=∠A=∠B,BC交PD于E,AD交PC于G,则图中