题目内容
3.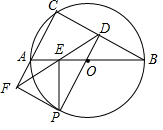 如图,⊙O是△ABC的外接圆,AB是直径,点D是弦BC的中点,延长DO交⊙O于点P,过点P作PE⊥AB于点E,作射线DE交CA的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AB是直径,点D是弦BC的中点,延长DO交⊙O于点P,过点P作PE⊥AB于点E,作射线DE交CA的延长线于F点,连接PF.(1)若∠B=30°,AB=10,求劣弧$\widehat{PC}$的长;(结果保留π)
(2)线段AE与AF相等吗?为什么?
(3)PF与⊙O的相切吗?为什么?
分析 (1)根据弧长计算公式l=$\frac{nπr}{180}$进行计算即可;
(2)证明△BOD≌△POE可得DO=EO,根据等腰三角形的性质得到∠ODE=∠OED,根据平行线的性质得到∠ODE=∠AFE,等量代换得到∠AEF=∠AFE,由等腰三角形的判定即可得到结论;
(3)连接AP,PB,证出PA为EF的中垂线,再利用△AEP∽△BAP找出角的关系求解.
解答 (1)解:连接OC,
∵点D是弦BC的中点,AB是直径,
∴OD⊥BC,
∵AB是直径,
∴∠BDO=∠C=90°,
∵∠ABC=30°,AB=10,
∴AO=5,∠AOC=∠BOD=60°,
∴∠POA=60°,
∴∠POC=120°,
∴$\widehat{PC}$的长=$\frac{120•π•5}{180}$=$\frac{10}{3}$π;
(2)证明:∵PE⊥AB,OD⊥CB,
∴∠PEO=90°,∠BDO=90°
在△BDO和△PEO中,$\left\{\begin{array}{l}{∠BOD=∠PEO}\\{∠BOD=∠POE}\\{OB=OP}\end{array}\right.$,
∴△POE≌△BOD(AAS),
∴OD=EO,
∴∠ODE=∠OED,
∵∠BDO=∠BCA=90°,
∴OD∥AC,
∴∠ODE=∠AFE,
∵∠DEO=∠AEF,
∴∠AEF=∠AFE,
∴AE=AF;
(3)证明:如图,连接AP,PB,
∵OB=OP,
∴∠OBP=∠OPB,
由(2)得OD=EO,
∴∠ODE=∠OED,
又∵∠BOP=∠EOD,
∴∠OPB=∠ODE,
∴BP∥DF,
∵AB是直径,
∴∠APB=90°,
∴∠PQE=90°
∴PA⊥EF,
∵AE=AF,
∴PA为EF的中垂线,
∴∠EPQ=∠QPF,
∵△AEP∽△BAP
∴∠EPQ=∠EBP,
∴∠QPF=∠EBP,
∴∠QPF=∠OPB,
∵∠OPB+∠OPA=90°,
∴∠QPF+∠OPA=90°,
∴OP⊥PF,
∴PF是⊙O的切线.
点评 本题主要考查了切线的判定,解题的关键是适当的作出辅助线,准确的找出角的关系.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | 矩形的两条对角线互相平分 | |
| B. | 平行四边形的两条对角线相等 | |
| C. | 菱形的两条对角线互相垂直 | |
| D. | 等腰三角形底边上的中点到两腰的距离相等 |
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -$\frac{1}{1017}$ | D. | 0 |
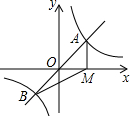 如图,函数y=kx(k≠0)与y=$\frac{3}{x}$的图象交于A,B两点,过点A作AM垂直于x轴,垂足为点M,则△BOM的面积为2.
如图,函数y=kx(k≠0)与y=$\frac{3}{x}$的图象交于A,B两点,过点A作AM垂直于x轴,垂足为点M,则△BOM的面积为2.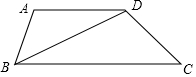 已知:如图,AD∥BC,∠A=∠BDC.
已知:如图,AD∥BC,∠A=∠BDC.