题目内容
14.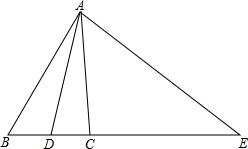 如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B.
如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B.(1)AD是∠BAC的平分线吗?为什么?
(2)若∠B=50°,∠E=40°,求∠ACE和∠ADC的度数.
分析 (1)由三角形外角的性质结合条件可得到∠EAC+∠DAC=∠B+∠BAD,可得出结论;
(2)在△ACE中由三角形内角和定理可求得∠ACE,在△AED中可求得∠ADC.
解答 解:(1)是.理由如下:
∵∠ADE是△ABD的外角,
∴∠ADE=∠B+∠BAD,
∵∠B=∠EAC,
∴∠ADE=∠EAC+∠BAD,
∵∠ADE=∠EAD=∠EAC+∠CAD,
∴∠BAD=∠CAD,
∴AD是∠BAC的角平分线;
(2)∵∠EAC=∠B,
∴∠EAC=50°,且∠E=40°,
∵∠EAC+∠E+∠ACE=180°,
∴∠ACE=180°-50°-40°=90°;
在△AED中,∵∠EAD=∠EDA,
∴∠EDA=$\frac{1}{2}$(180°-∠E)=$\frac{1}{2}$×(180°-40°)=70°,
即∠ADC=70°.
点评 本题主要考查三角形内角和定理.掌握三角形内角和为180°,能够灵活运用该定理是解题的关键.

练习册系列答案
相关题目
5.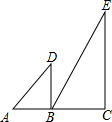 如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )
如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )
 如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )
如图,直线AC的同侧有Rt△ABD和Rt△BCE,已知∠ABD=∠C=90°,∠A=45°,∠E=30°.若△ABD绕点B顺时针方向旋转,当两个三角形有一边平行时,旋转的角度(小于180°)是( )| A. | 90° | B. | 45° | C. | 45°或90° | D. | 45°或90°或135° |
3.下列运算正确的是( )
| A. | 3x2+2x3=5x6 | B. | (x3)2=x6 | C. | ${3}^{-2}=\frac{1}{6}$ | D. | 50=0 |
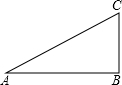 利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.
利用勾股定理,可以作出长为$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的线段,如图:在Rt△ABC中,AB=2,BC=1,则AC的长等于$\sqrt{5}$.在按同样的方法,可以在数轴上画出表示$\sqrt{2}$、$\sqrt{3}$、$\sqrt{5}$、…的点.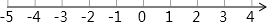
 如图,已知CD垂直平分AB,AB平分∠CAD,试说明CB∥AD.
如图,已知CD垂直平分AB,AB平分∠CAD,试说明CB∥AD.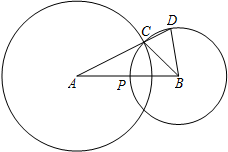 已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.
已知:如图,C是⊙A与⊙B的一个交点,联结AC,并延长交⊙B于点D,⊙B交AB于点P,联结BC、BD,AB=8,AC=6,⊙B的半径为x,线段AD的长为y.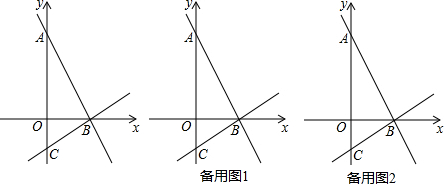
 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD的面积为24.
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD的面积为24.