题目内容
4. 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD的面积为24.
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD的面积为24.
分析 由平行四边形的性质求出OA、OB,再证明△AOB是直角三角形,证出AC⊥DB,得出四边形ABCD是菱形,菱形的面积=两条对角线长乘积的一半,即可得出结果.
解答 解∵四边形ABCD是平行四边形,
∴OA=$\frac{1}{2}$AC=3,OB=$\frac{1}{2}$DB=4,
∵OA2+OB2=AB2,
∴△AOB是直角三角形,
∴∠AOB=90°,
∴AC⊥DB,
∴四边形ABCD是菱形,
∴四边形ABCD的面积=$\frac{1}{2}$AC•DB=$\frac{1}{2}$×6×8=24;
故答案为:24.
点评 本题考查了平行四边形的性质、直角三角形的判定、菱形的判定;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
15.一次函数y=2x-6的图象经过( )
| A. | 第一、二、三象限 | B. | 第一、三、四象限 | C. | 第一、二、四象限 | D. | 第二、三、四象限 |
16.要使分式$\frac{4}{x-2}$有意义,则x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≠2 | D. | x≥2 |
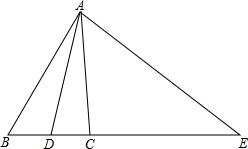 如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B.
如图所示,在△ABC中,∠EAD=∠EDA,∠EAC=∠B. 如图所示的图案绕其旋转中心旋转后能够与自身重合,那么它的旋转角的度数可能是72°(答案不唯一)(填写一个你认为正确的答案).
如图所示的图案绕其旋转中心旋转后能够与自身重合,那么它的旋转角的度数可能是72°(答案不唯一)(填写一个你认为正确的答案).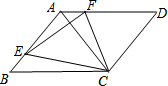 已知,如图,在菱形ABCD中,∠B=60°,菱形ABCD的面积为50$\sqrt{3}$,点E、F分别在AB、AD上,且BE=AF=2,则△ECF的周长为6$\sqrt{21}$.
已知,如图,在菱形ABCD中,∠B=60°,菱形ABCD的面积为50$\sqrt{3}$,点E、F分别在AB、AD上,且BE=AF=2,则△ECF的周长为6$\sqrt{21}$. ,实际时间是16:25:08.
,实际时间是16:25:08.