题目内容
已知抛物线y=a(x-1)(x-2)经过点(-1,3).
(1)求抛物线的解析式并画出函数图象;
(2)写出抛物线的对称轴和顶点坐标;
(3)当x为何值时,函数y>0?
(1)求抛物线的解析式并画出函数图象;
(2)写出抛物线的对称轴和顶点坐标;
(3)当x为何值时,函数y>0?
考点:二次函数的性质,二次函数的图象
专题:
分析:(1)将点(-1,3)代入y=a(x-1)(x-2),利用待定系数法即可求出抛物线的解析式,再画出函数图象;
(2)利用配方法将解析式化为顶点式,即可求出对称轴和顶点坐标;
(3)根据图象即可得出x<1或x>2时,函数y>0.
(2)利用配方法将解析式化为顶点式,即可求出对称轴和顶点坐标;
(3)根据图象即可得出x<1或x>2时,函数y>0.
解答: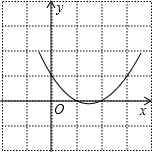 解:(1)∵抛物线y=a(x-1)(x-2)经过点(-1,3),
解:(1)∵抛物线y=a(x-1)(x-2)经过点(-1,3),
∴3=6a,解得a=
,
∴抛物线的解析式为y=
(x-1)(x-2),
图象如图所示:
(2)∵y=
(x-1)(x-2)
=
(x2-3x+2)
=
(x-
)2-
,
∴抛物线的对称轴为x=
,顶点坐标为(
,-
);
(3)由图象可知,当x<1或x>2时,函数y>0.
 解:(1)∵抛物线y=a(x-1)(x-2)经过点(-1,3),
解:(1)∵抛物线y=a(x-1)(x-2)经过点(-1,3),∴3=6a,解得a=
| 1 |
| 2 |
∴抛物线的解析式为y=
| 1 |
| 2 |
图象如图所示:
(2)∵y=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
∴抛物线的对称轴为x=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 8 |
(3)由图象可知,当x<1或x>2时,函数y>0.
点评:本题主要考查待定系数法求二次函数解析式和二次函数的图象的知识点,本题需要有较强的作图能力,熟练掌握二次函数的性质是解答本题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、有一条公共边的两个全等三角形关于共边所在的直线对称 |
| B、全等三角形是关于某直线对称的 |
| C、两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧 |
| D、关于某直线对称的两个三角形是全等三角形 |
 已知,如图在△ABC中,BC=6,AC=8,DE是AB边上的高,DE=7,△ABE的面积为35.求四边形ACBE的面积.
已知,如图在△ABC中,BC=6,AC=8,DE是AB边上的高,DE=7,△ABE的面积为35.求四边形ACBE的面积.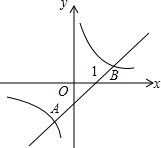 如图,反比例函数y=
如图,反比例函数y= 如图,∠ACB=90°,CD⊥AB于点D,AE平分∠BAC,交CD于点E,过E作EF∥BC,交AB于点F,求证:△ACE≌△AFE.
如图,∠ACB=90°,CD⊥AB于点D,AE平分∠BAC,交CD于点E,过E作EF∥BC,交AB于点F,求证:△ACE≌△AFE.