题目内容
 如图,∠ACB=90°,CD⊥AB于点D,AE平分∠BAC,交CD于点E,过E作EF∥BC,交AB于点F,求证:△ACE≌△AFE.
如图,∠ACB=90°,CD⊥AB于点D,AE平分∠BAC,交CD于点E,过E作EF∥BC,交AB于点F,求证:△ACE≌△AFE.考点:全等三角形的判定
专题:证明题
分析:求出∠CAE=∠FAE,根据平行线的性质和三角形内角和定理求出∠B=∠ACE=∠AFE,根据AAS推出两三角形全等即可.
解答:证明:∵AE平分∠CAB,
∴∠CAE=∠FAE,
∵CD⊥AB,∠ACB=90°,
∴∠CDB=∠ACB=90°,
∴∠B+∠BCD=90°,∠BCD+∠ACE=90°,
∴∠B=∠ACE,
∵EF∥BC,
∴∠AFE=∠B,
∴∠AFE=∠ACE,
在△ACE和△AFE中
∴△ACE≌△AFE.
∴∠CAE=∠FAE,
∵CD⊥AB,∠ACB=90°,
∴∠CDB=∠ACB=90°,
∴∠B+∠BCD=90°,∠BCD+∠ACE=90°,
∴∠B=∠ACE,
∵EF∥BC,
∴∠AFE=∠B,
∴∠AFE=∠ACE,
在△ACE和△AFE中
|
∴△ACE≌△AFE.
点评:本题考查了三角形内角和定理,平行线的性质,全等三角形的性质和判定的应用,解此题的关键是求出∠ACE=∠AFE.

练习册系列答案
相关题目
 如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙O上运动一周,点D运动的路径长为
如图,AB为⊙O的直径,AB=8,点C为圆上任意一点,OD⊥AC于D,当点C在⊙O上运动一周,点D运动的路径长为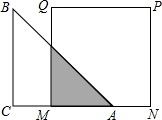 如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积y cm2与MA的长度x cm之间的关系式,并指出其中的常量与变量.
如图,等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分的面积y cm2与MA的长度x cm之间的关系式,并指出其中的常量与变量.