Question

17．已知抛物线y=-x²+2mx-m²+3m+1的顶点为M，不论m为何值，顶点M均在某一直线l上．
（1）求此直线l的函数解析式；
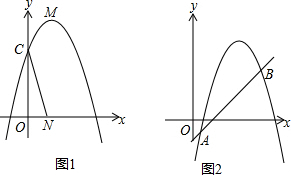
（2）当m=1时，点N（1，0），抛物线与y轴交于点C，点P是第一象限抛物线上一点，使得线段OP与直线CN的夹角为45°，求点P的坐标；
（3）是否存在直线y=kx-3与抛物线交于A、B两点（A点在B点的下方），使AB为定长？若存在，求出k的值和AB的长；若不存在，请说明．

Answer 1

分析 （1）利用配方法求出顶点M的坐标，即可解决问题．
（2）如图1中，先求出直线CN解析式，设CP交CN于Q，Q（n，-3n+3），作OD⊥OP交CN于D，作QH⊥y轴于H，DG⊥y轴于G．由△OHQ≌△DGO，
得OG=QH=n，DG=OH=-3n+3，得出点D坐标代入抛物线解析式即可解决问题．
（3）设A（x₁，kx₁-3），B（x₂，kx₂-3），由$\left\{\begin{array}{l}{y=kx-3}\\{y=-{x}^{2}+2mx-{m}^{2}+3m+1}\end{array}\right.$，消去y得到x²-（2m-k）x+m²-3m-4=0，得x₁+x₂=2m-k，x₁•x₂=m²-3m-4，所以AB²=（x₁-x₂）²+（kx₁-kx₂）²=（1+k²）[（x₁+x₂）²-4x₁x₂]=（1+k²）[2m-k）²-4（m²-3m-4）]=（1+k²）[（12-4k）m+k²+16]，因为AB的为定长，所以AB的长与m无关，
得到方程12-4k=0，即可解决问题．

解答 解：（1）∵y=-x²+2mx-m²+3m+1=-（x-m）²+3m+1，
∴顶点M坐标（m，3m+1），
∴顶点M在直线y=3x+1上．

（2）如图1中，

∵m=1，
∴抛物线解析式为y=-x²+2x+3，
令x=0，得y=3，
∴C坐标（0，1），
∵N（1，0），
∴可得直线CN解析式为：y=-3x+3．设CP交CN于Q，Q（n，-3n+3），
作OD⊥OP交CN于D，
∵∠OQD=45°，
∴△OQD是等腰直角三角形，作QH⊥y轴于H，DG⊥y轴于G，
∵∠QOD=∠QHO=∠DGO=90°，
∴∠QOH+∠DOG=90°，∠QOH+∠OQH=90°，
∴∠QOH=∠DOG，
在△OQH和△DOG中，
$\left\{\begin{array}{l}{∠QOH=∠DOG}\\{∠QHO=∠DGO}\\{OQ=OD}\end{array}\right.$，
∴△OHQ≌△DGO，
∴OG=QH=n，DG=OH=-3n+3，
∴D（-3n+3，-n）代入y=-3x+3中，-n=-3（-3n+3）+3，
∴n=$\frac{3}{5}$，
∴Q（$\frac{3}{5}$，$\frac{6}{5}$），
∴直线OP解析式为y=2x，
由$\left\{\begin{array}{l}{y=2x}\\{y=-{x}^{2}+2x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=2\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\sqrt{3}}\\{y=-2\sqrt{3}}\end{array}\right.$（舍弃），
∴点P坐标（$\sqrt{3}$，2$\sqrt{3}$）．

（3）设A（x₁，kx₁-3），B（x₂，kx₂-3），
由$\left\{\begin{array}{l}{y=kx-3}\\{y=-{x}^{2}+2mx-{m}^{2}+3m+1}\end{array}\right.$，消去y得到x²-（2m-k）x+m²-3m-4=0，
∴x₁+x₂=2m-k，x₁•x₂=m²-3m-4，
∵AB²=（x₁-x₂）²+（kx₁-kx₂）²
=（1+k²）[（x₁+x₂）²-4x₁x₂]
=（1+k²）[2m-k）²-4（m²-3m-4）]
=（1+k²）[（12-4k）m+k²+16]，
∵AB的为定长，
∴AB的长与m无关，
∴12-4k=0，
∴k=3，
∴AB²=（1+3²）×（9+16）=250，
∵AB＞0，
∴AB=5$\sqrt{10}$．

点评 本题考查二次函数综合题、一次函数、全等三角形的判定和性质、两点间距离公式、定长问题等知识，解题的关键是学会添加常用辅助线，构造全等三角形，学会利用参数解决问题，掌握求定长问题的方法，所以中考压轴题．