题目内容
2.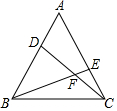 如图,在等边△ABC中,点D在边AB上,点E在边AC上,∠A=60°,且AD=CE,BE与CD相交于F,则∠BFC的度数为120°.
如图,在等边△ABC中,点D在边AB上,点E在边AC上,∠A=60°,且AD=CE,BE与CD相交于F,则∠BFC的度数为120°.
分析 根据等边三角形的性质得到∠A=∠BCE=60°,AC=BC,而AD=CE,根据全等三角形的判定得到△ACD≌△CBE,得到∠ACD=∠CBE,而∠ACD+∠FCB=60°,则∠CBE+∠FCB=60°,根据三角形的内角和定理即可得到∠BFC的度数.
解答 证明:∵△ABC是等边三角形,
∴∠A=∠BCE=60°,AC=BC,
在△ACD和△CBE中,
$\left\{\begin{array}{l}{AD=CE}\\{∠A=∠BCE}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△CBE;
∴∠ACD=∠CBE,
而∠ACD+∠FCB=60°,
∴∠CBE+∠FCB=60°,
∴∠BFC=180°-(∠CBE+∠FCB)=180°-60°=120°.
故答案为120°.
点评 本题考查了全等三角形的判定与性质:有两组对应边相等,并且它们的夹角也相等的两个三角形全等;全等三角形的对应角相等.也考查了等边三角形的性质.

练习册系列答案
相关题目
7.在x=0,-$\frac{5}{2}$,3,$\frac{5}{3}$中,满足不等式组$\left\{\begin{array}{l}{\frac{x}{2}<1}\\{2(x+1)>-2}\end{array}\right.$的x值是( )
| A. | 0和-$\frac{5}{2}$ | B. | -$\frac{5}{2}$和$\frac{5}{3}$ | C. | 0和3 | D. | 0和$\frac{5}{3}$ |
12.某教育主管部门深入边远山区,随机走访农户,调查农村儿童生活教育现状,根据收集的数据编制了不完整的统计图表如下:
山区儿童生活教育现状
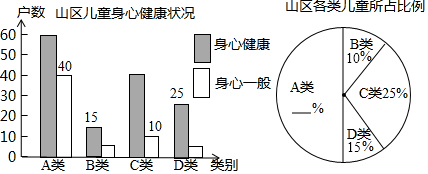
请你用学过的统计知识,解决问题:
(1)教育主管部门走访了边远山区多少家农户?
(2)将统计图表中的空缺数据填写完整;
(3)分析数据后,请你提一条合理建议.
山区儿童生活教育现状
| 类别 | 现状 | 户数 | 比例 |
| A类 | 父母长年在外打工,孩子留在老家由老人照顾 | 100 | |
| B类 | 父母长年在外打工,孩子带在身边 | 10% | |
| C类 | 父母就近在城镇打工,晚上回家照顾孩子 | 50 | |
| D类 | 父母在家务农,并照顾孩子 | 15% |

请你用学过的统计知识,解决问题:
(1)教育主管部门走访了边远山区多少家农户?
(2)将统计图表中的空缺数据填写完整;
(3)分析数据后,请你提一条合理建议.
 小明在做课本“目标与评定”中的一道题:如图(1),直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图(1),画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.
小明在做课本“目标与评定”中的一道题:如图(1),直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小明的做法是:如图(1),画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.