题目内容
观察下列等式:
第1个等式:a1=
=
×(1-
)
第2个等式:a2=
=
×(
-
)
第3个等式:a3=
=
×(
-
)
第4个等式:a4=
=
×(
-
)
…请回答下列问题:
(1)按以上规律用含有n的代数式表示第n个等式:an= (n为正整数).
(2)求a1+a2+a3+…+an的值.
第1个等式:a1=
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
第2个等式:a2=
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
第3个等式:a3=
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
第4个等式:a4=
| 1 |
| 7×9 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 9 |
…请回答下列问题:
(1)按以上规律用含有n的代数式表示第n个等式:an=
(2)求a1+a2+a3+…+an的值.
考点:规律型:数字的变化类
专题:
分析:(1)观察知,找第一个等号后面的式子规律是关键:分子不变,为1;分母是两个连续奇数的乘积,它们与式子序号之间的关系为 序号的2倍减1和序号的2倍加1.
(2)运用(1)的变化规律计算.
(2)运用(1)的变化规律计算.
解答:解:(1)an=
=
×(
-
);
(2)a1+a2+a3+…+an
=
×(1-
)+
×(
-
)+
×(
-
)+
×(
-
)+…+
×(
-
)
=
×(1-
+
-
+
-
+
-
+…+
-
)
=
×(1-
)
=
.
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
(2)a1+a2+a3+…+an
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 9 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
=
| n |
| 2n+1 |
点评:此题考查寻找数字的规律及运用规律计算.寻找规律大致可分为2个步骤:不变的和变化的;变化的部分与序号的关系.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
下列四个图形中,是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
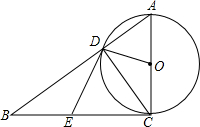 如图,以△ABC的边AC为直径的⊙O与BC相切于点C,⊙O与AB相交于点D,E是BC的中点.
如图,以△ABC的边AC为直径的⊙O与BC相切于点C,⊙O与AB相交于点D,E是BC的中点.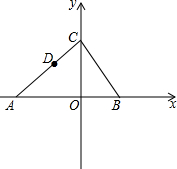 如图,点A、B的坐标分别是(-5,0),(3,0),C的坐标为(0,4),点D在线段AC上,且S△AOD=
如图,点A、B的坐标分别是(-5,0),(3,0),C的坐标为(0,4),点D在线段AC上,且S△AOD=