题目内容
1．
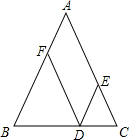如图，等腰△ABC中，AB=AC，?AFDE的顶点D、E、F分别在边BC、AC、AB上，如果?AFDE的周长为30，那么等腰△AEC的腰长为（ ）| A． | 30 | B． | 25 | C． | 20 | D． | 15 |
分析 根据等腰三角形的性质可得到两底角相等，再根据平行四边形的性质可推出DE=EC，根据平行四边形的周长公式不难求解．
解答 解：∵AB=AC，
∴∠B=∠C，
∵DE∥AB，
∴∠B=∠EDC，
∴DE=EC，
∵四边形AEDF是平行四边形，
∴DE=AF，
∴AF=CE，
∴?AEDF的周长=2（AF+AE）=2AC=30，
∴AB=AC=15，
故选D．
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质．此题难度不大，解题的关键是得到?AEDF的周长=2（AF+AE）=2AC．
练习册系列答案
相关题目
11．在Rt△ABC中，∠C=90°，如果三角形各边的长度都扩大2倍，则sinA的值（ ）
| A． | 不变 | B． | 扩大2倍 | C． | 缩小2倍 | D． | 不能确定 |
把一个长方形纸片按如图所示折叠，若量得∠AOD′=32°，则∠D′OE=74°．
如图，点E，F，G，H分别在矩形ABCD的四条边AD，AB，BC，CD上，若∠AEF=20°，∠EFG=∠FGH=90°，则∠GHD=110°．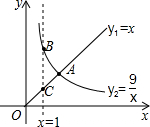
函数y1=x（x≥0），y2=$\frac{9}{x}$（x＞0）的图象如图所示，则下列结论：
13．下列各式计算正确的是（ ）
| A． | -32=-9 | B． | -（-3）2=9 | C． | （-3）2=6 | D． | （-1）3=1 |
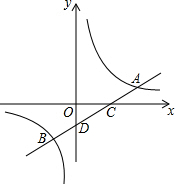在平面直角坐标系内，点O为坐标原点，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A，B两点，若A（4，1），点B的横坐标为-2．