题目内容
6.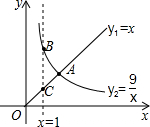 函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则下列结论:
函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则下列结论:①两函数图象的交点A的坐标为(3,3);②当x>3时,y1>y2;③当x=1时,BC=8;④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.
其中正确结论的序号是①②③④.
分析 ①联立两函数解析式,解方程组,再根据交点A在第一象限即可确定;
②根据函数图象在上方的函数的值大于在下方的函数的值解答;
③利用两个函数的解析式分别求出x=1时的函数值,相减即可得到BC的长度;
④分别根据一次函数的增减性与反比例函数的增减性进行判断.
解答 解:①联立$\left\{\begin{array}{l}{y=x}\\{y=\frac{9}{x}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=-3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=3}\end{array}\right.$,
∵点A在第一象限,
∴两函数图象的交点A的坐标为(3,3 ),故本小题正确;
②由图象可知,当x>3时,y1>y2,故本小题正确;
③当x=1时,yl=1,y2=$\frac{9}{1}$=9,
所以,BC=9-1=8,故本小题正确;
④根据图象,当x逐渐增大时,yl随着x的增大而增大,y2随着x的增大而减小,故本小题正确;
综上,正确的结论是①②③④.
故答案为:①②③④.
点评 本题综合考查了一次函数与反比例函数的交点问题,已知自变量求函数值,联立两函数解析式求交点,数形结合利用图象求不等式的解,一次函数与反比例函数的增减性,综合题,但难度不大,都是基础知识.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
17.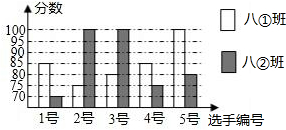 某中学开展“我为文明城市创建添光彩”演讲比赛活动,八①班、八②班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
某中学开展“我为文明城市创建添光彩”演讲比赛活动,八①班、八②班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
(1)将上表填写完整;
(2)结合两班复赛成绩和平均数和中位数,分析哪个班的复赛成绩比较好?
(3)如果在每班参加复赛的选手中分别选车2人参加决赛,你认为哪个班的实力更强一些,并说明理由.
 某中学开展“我为文明城市创建添光彩”演讲比赛活动,八①班、八②班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
某中学开展“我为文明城市创建添光彩”演讲比赛活动,八①班、八②班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:| 班级 | 平均数 (分) | 中位数 (分) | 众数 (分) |
| 八①班 | 85 | 85 | 85 |
| 八②班 | 85 | 80 | 100 |
(2)结合两班复赛成绩和平均数和中位数,分析哪个班的复赛成绩比较好?
(3)如果在每班参加复赛的选手中分别选车2人参加决赛,你认为哪个班的实力更强一些,并说明理由.
11.下列说法中正确的是( )
| A. | +(-3)的相反数是-3 | B. | -(+6)的相反数是-6 | ||
| C. | 整数的相反数一定是整数 | D. | 0没有相反数 |
18.两个有理数的商是正数,关于这两个有理数下面判断正确是( )
| A. | 和是正数 | B. | 差是正数 | C. | 积是正数 | D. | 以上都不对 |
15.12的负平方根介于( )
| A. | -5和-4之间 | B. | -3和-2之间 | C. | -4和-3之间 | D. | -2和-1之间 |
16.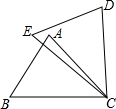 如图,在△ABC和△DEC中,已知AB=DE,补充下列一组条件,仍无法判定△ABC≌△DEC的是( )
如图,在△ABC和△DEC中,已知AB=DE,补充下列一组条件,仍无法判定△ABC≌△DEC的是( )
 如图,在△ABC和△DEC中,已知AB=DE,补充下列一组条件,仍无法判定△ABC≌△DEC的是( )
如图,在△ABC和△DEC中,已知AB=DE,补充下列一组条件,仍无法判定△ABC≌△DEC的是( )| A. | BC=EC,∠B=∠E | B. | BC=EC,AC=DC | C. | ∠B=∠E,∠A=∠D | D. | BC=EC,∠A=∠D |
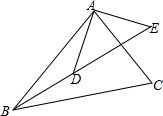 如图所示,E是△ABC外一点,D在BE上,且∠BAD=20°,$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,求∠EBC的度数.
如图所示,E是△ABC外一点,D在BE上,且∠BAD=20°,$\frac{AB}{AD}=\frac{BC}{DE}=\frac{AC}{AE}$,求∠EBC的度数.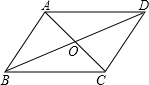 如图,在?ABCD中,AC,BD相交于点O,若AC=6cm,BD=8cm,BC=5cm,则△BOC的周长是12cm.
如图,在?ABCD中,AC,BD相交于点O,若AC=6cm,BD=8cm,BC=5cm,则△BOC的周长是12cm.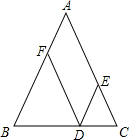 如图,等腰△ABC中,AB=AC,?AFDE的顶点D、E、F分别在边BC、AC、AB上,如果?AFDE的周长为30,那么等腰△AEC的腰长为( )
如图,等腰△ABC中,AB=AC,?AFDE的顶点D、E、F分别在边BC、AC、AB上,如果?AFDE的周长为30,那么等腰△AEC的腰长为( )