题目内容
如图，E、F分别是平行四边形ABCD的边AD、BC的中点，若四边形AEFB与四边形ABCD相似，AB=4，则AD的长度为考点：相似多边形的性质
专题：
分析：首先设AE=x，则AD=2x，进而利用四边形ABCD与四边形ABFE是相似的，则
=
，进而求出即可．
| AE |
| AB |
| AB |
| AD |
解答：解：设AE=x，则AD=2x，
∵四边形ABCD与矩四边形ABFE是相似的，
∴
=
，
∴AB2=2x2，
∴AB=
x=4，
∴x=2
，
∴AD=4
，
故答案为：4
．
∵四边形ABCD与矩四边形ABFE是相似的，
∴
| AE |
| AB |
| AB |
| AD |
∴AB2=2x2，
∴AB=
| 2 |
∴x=2
| 2 |
∴AD=4
| 2 |
故答案为：4
| 2 |
点评：此题主要考查了相似多边形的性质，表示出AB的长是解题关键．
练习册系列答案
相关题目
如图，△ABC中，∠A=40°∠B=76°，CE平分∠ACB，CD⊥AB于点D，DF⊥CE于点F，求∠CDF的度数．比较大小，正确的是（ ）
| A、-2＜-3 | ||||
B、-
| ||||
| C、-3＜2 | ||||
| D、2＜-3 |
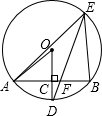如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．
如图，在△ABC中，∠ACB=90°，点D在BC的延长线上，点E在AB上，DE交AC于点F，ED=EB．求证：AE=EF．下列说法中，正确的是（ ）
| A、-81的平方根是±9 | ||
| B、-6是（-6）2的平方根 | ||
C、
| ||
D、
|