题目内容
15. 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两只等腰直角三角形纸片的面积都为m,另两张直角三角形纸片的面积都为n,中间一张正方形纸片的面积为1,则这个平行四边形的面积一定可以表示为( )
如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两只等腰直角三角形纸片的面积都为m,另两张直角三角形纸片的面积都为n,中间一张正方形纸片的面积为1,则这个平行四边形的面积一定可以表示为( )| A. | 4m | B. | 4n | C. | 4n+1 | D. | 3m+4 |
分析 设等腰直角三角形的直角边为a,正方形边长为c,求出S2(用a、c表示),得出S1,S2,S3之间的关系,由此即可解决问题.
解答 解:设等腰直角三角形的直角边为a,正方形边长为c,
则S2=$\frac{1}{2}$(a+c)(a-c)=$\frac{1}{2}$a2-$\frac{1}{2}$c2,
∴S2=S1-$\frac{1}{2}$S3,
∴S3=2S1-2S2,
∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1-2S2=4S1=4m,
故选A.
点评 本题考查平行四边形的性质、直角三角形的面积等知识,解题的关键是求出S1,S2,S3之间的关系,属于中考常考题型.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | 20=0 | B. | a•2a=3a | C. | (ab2)3=3a3b6 | D. | 2a6÷a-2=2a8 |
6.-$\frac{5}{3}$的倒数的相反数是( )
| A. | $\frac{5}{3}$ | B. | -$\frac{5}{3}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
3.一次考试中,某班85%的同学数学成绩不低于95分,下面一定不低于95的是( )
| A. | 全班数学成绩的平均数 | B. | 全班数学成绩的众数 | ||
| C. | 全班数学成绩的中位数 | D. | 无法确定 |
10.一列动车以300km/h的速度过第一、第二两个隧道,已知第二个隧道的长度比第一个隧道长度的2倍还多1.5km,已知该列动车过第二个隧道比第一个隧道多用了93秒,若设第一个隧道的长度为x km,则由题意列出的方程正确的是( )
| A. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-93 | B. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+93 | ||
| C. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$-$\frac{93}{3600}$ | D. | $\frac{x}{300}$=$\frac{2x+1.5}{300}$+$\frac{93}{3600}$ |
20.直线y=-3x+1不经过第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
7.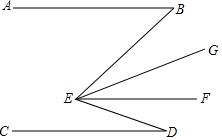 已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )
已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )
 已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )
已知:如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 20° |
4.若二次函数y=x2-4x+c的图象与x轴没有交点,其中c为常数,则c的取值范围是( )
| A. | c<4 | B. | c≤4 | C. | c>4 | D. | c≥4 |
5.下列事件中属于不可能事件的为( )
| A. | 掷一枚硬币10次,有10次正面朝上 | |
| B. | 任意画一个三角形,其内角和是360° | |
| C. | 汽车经过城市中一段路,途径5个交通信号灯的路口,经过时没遇上红灯 | |
| D. | 掷骰子100次,有100次点数是6的面朝上 |