题目内容
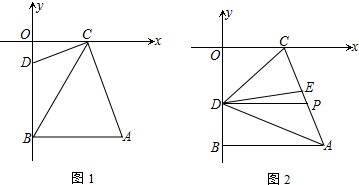
10.如图1,在平面直角坐标系中,A是第四象限内一点,AB⊥y轴于B,且C(3,0)是x轴正半轴上一点,OB-OC=2,S四边形ABOC=20.(1)求A的坐标;
(2)设D是线段OB上一动点,当∠CDO=∠A时,CD与AC之间存在怎样的位置关系,写出你的结论并证明;
(3)当D在线段OB上运动时,连接AD、CD,如图2,∠OCD>∠BAD,DE平分∠ADC,DP∥AB,$\frac{∠OCD-∠BAD}{∠PDE}$是否为定值?不是,请说明理由;是,请证明之.
分析 (1)首先判断四边形ABOC是直角梯形,根据梯形的面积公式求出AB,即可解决问题.
(2)利用四边形内角和360°,以及对角互补解决.
(3)根据平行线的性质以及角平分线的定义即可解决问题.
解答 解:(1)∵C(3,0),OB-OC=2,
∴OC=3,OB=5,
∵AB⊥y轴,
∴OC∥AB,
∴四边形ABOC是直角梯形,
∴$\frac{3+AB}{2}×5=20$,
∴AB=5,
∴点A坐标(5,-5).
(2)如图1中,结论:AC⊥CD.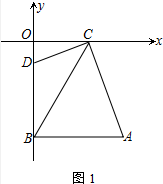
理由:
∵∠CDO+∠CDB=180°,∠CDO=∠A,
∴∠A+∠CDB=180°,
在四边形ABDC中,∵∠A+∠BDC+∠ABD+∠ACD=360°,
∴∠ABD+∠ACD=180°,
∵∠ABD=90°,
∴∠ACD=90°,
∴AC⊥CD.
(3)如图2中,结论:$\frac{∠OCD-∠BAD}{∠PDE}$=2.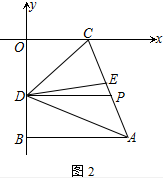
理由:∵OC∥DP,AB∥OC,
∴DP∥AB,
∴∠OCD=∠CDP=∠CDE+∠PDE,∠BAD=∠ADP=∠ADE-∠PDE,
∵DE平分∠CDA,
∴∠CDE=∠ADE,
∴∠OCD-∠BAD=(∠CDE+∠PDE)-(∠ADE-∠PDE)=2∠PDE,
∴$\frac{∠OCD-∠BAD}{∠PDE}$=$\frac{2∠PDE}{∠PDE}$=2.
点评 本题考查了坐标与图形性质、四边形内角和定理、平行线的性质、梯形的面积公式等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
20.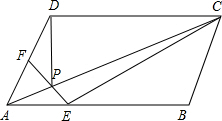 已知平行四边形ABCD中,E,F分别是AB,AD上的点,EF与对角线AC交于P,若$\frac{AE}{EB}$=$\frac{1}{2}$,$\frac{AF}{FD}$=$\frac{2}{3}$,则$\frac{{S}_{△PAD}}{{S}_{△PCE}}$的值为( )
已知平行四边形ABCD中,E,F分别是AB,AD上的点,EF与对角线AC交于P,若$\frac{AE}{EB}$=$\frac{1}{2}$,$\frac{AF}{FD}$=$\frac{2}{3}$,则$\frac{{S}_{△PAD}}{{S}_{△PCE}}$的值为( )
 已知平行四边形ABCD中,E,F分别是AB,AD上的点,EF与对角线AC交于P,若$\frac{AE}{EB}$=$\frac{1}{2}$,$\frac{AF}{FD}$=$\frac{2}{3}$,则$\frac{{S}_{△PAD}}{{S}_{△PCE}}$的值为( )
已知平行四边形ABCD中,E,F分别是AB,AD上的点,EF与对角线AC交于P,若$\frac{AE}{EB}$=$\frac{1}{2}$,$\frac{AF}{FD}$=$\frac{2}{3}$,则$\frac{{S}_{△PAD}}{{S}_{△PCE}}$的值为( )| A. | $\frac{3}{7}$ | B. | $\frac{2}{3}$ | C. | $\frac{18}{13}$ | D. | $\frac{18}{7}$ |
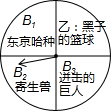 周助是个动漫迷,妈妈用周助喜欢的动漫设计了下面的游戏:用如图被平均分成4份的转盘,转动转盘,转盘静止后,指针指向一个动漫名.若所指的动漫名不在文化部动漫黑名单内,则周助每天可以看一集动漫;否则,周助三天才可以看一集动漫.(注:B系列在文化部动漫黑名单内)
周助是个动漫迷,妈妈用周助喜欢的动漫设计了下面的游戏:用如图被平均分成4份的转盘,转动转盘,转盘静止后,指针指向一个动漫名.若所指的动漫名不在文化部动漫黑名单内,则周助每天可以看一集动漫;否则,周助三天才可以看一集动漫.(注:B系列在文化部动漫黑名单内)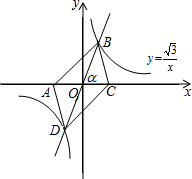 如图,在平面直角坐标系中,将x轴所在的直线绕着原点O按逆时针方向旋转α角度后,这条直线与函数y=$\frac{\sqrt{3}}{x}$的图象分别交于点B、D,已知点A(-m,0),C(m,0)且m≠0.
如图,在平面直角坐标系中,将x轴所在的直线绕着原点O按逆时针方向旋转α角度后,这条直线与函数y=$\frac{\sqrt{3}}{x}$的图象分别交于点B、D,已知点A(-m,0),C(m,0)且m≠0.