题目内容
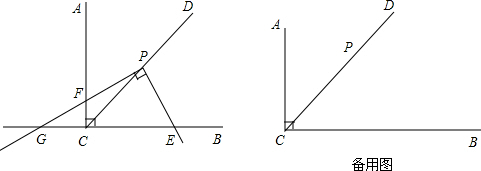
已知,∠ACB=90°,CD是∠ACB的平分线,点P在CD上,CP=2.将三角板的直角顶点放置在点P处,绕着点P旋转,三角板的一条直角边与射线CB交于点E,另一条直角边与直线CA、直线CB分别交于点F、点G.试探索:在旋转过程中四边形PFCE的面积是否会发生改变?若不变,请求出这个面积;若改变,请说明理由.

考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:作PM⊥AC,PN⊥BC,即可求证△MPF≌△NPE,即可求证四边形PFCE的面积=正方形PMCN的面积,即可解题.
解答:解:作PM⊥AC,PN⊥BC,

∵P是CD上点,∴PM=PN,
PM=PN,
∵∠MPN=90°,∠FPE=90°,
∴∠MPF=∠NPE,
在△MPF和△NPE中,
,
∴△MPF≌△NPE(AAS),
∴四边形PFCE的面积=正方形PMCN的面积,
∵CP=2,
∴CM=PM=
,
∴四边形PFCE的面积=正方形PMCN的面积=CM•PM=2.
答:在旋转过程中,四边形PFCE的面积不会改变,且四边形PFCE的面积=2.

∵P是CD上点,∴PM=PN,
PM=PN,
∵∠MPN=90°,∠FPE=90°,
∴∠MPF=∠NPE,
在△MPF和△NPE中,
|
∴△MPF≌△NPE(AAS),
∴四边形PFCE的面积=正方形PMCN的面积,
∵CP=2,
∴CM=PM=
| 2 |
∴四边形PFCE的面积=正方形PMCN的面积=CM•PM=2.
答:在旋转过程中,四边形PFCE的面积不会改变,且四边形PFCE的面积=2.
点评:本题考查了全等三角形的判定,考查了全等三角形面积相等的性质,本题中求证△MPF≌△NPE是解题的关键.

练习册系列答案
相关题目
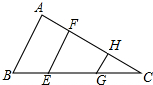 如图,AB∥EF∥GH,BE=CG,求证:AB=EF+GH.
如图,AB∥EF∥GH,BE=CG,求证:AB=EF+GH.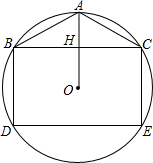 已知,如图,矩形BCED的两个顶点在⊙O上,过O作BC的垂线交BC于H,交⊙O于A,连AB,AC.
已知,如图,矩形BCED的两个顶点在⊙O上,过O作BC的垂线交BC于H,交⊙O于A,连AB,AC. 从角的顶点出发,把这个角分成相等的两个角的射线,叫作这个角的
从角的顶点出发,把这个角分成相等的两个角的射线,叫作这个角的