题目内容
已知:如图,数轴上点A表示的数为6,点B表示的数为2,点C表示的数为-8,动点P从点A出发,沿数轴向左运动,速度为每秒1个单位长度.点M为线段BC中点,点N为线段BP中点.设运动时间为t秒.
(1)线段AC的长为 个单位长度;点M表示的数为 ;
(2)当t=5时,求线段MN的长度;
(3)在整个运动过程中,求线段MN的长度.(用含t的式子表示).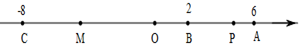
(1)线段AC的长为
(2)当t=5时,求线段MN的长度;
(3)在整个运动过程中,求线段MN的长度.(用含t的式子表示).
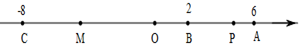
考点:两点间的距离,数轴
专题:
分析:(1)根据两点间的距离公式可得AC=6-(-8),根据中点坐标公式可得M点表示的数为-8+
[2-(-8)];
(2)当t=5时,可得P表示的数,再根据中点坐标公式可得N点表示的数,再根据两点间的距离公式可得线段MN的长度;
(3)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.
| 1 |
| 2 |
(2)当t=5时,可得P表示的数,再根据中点坐标公式可得N点表示的数,再根据两点间的距离公式可得线段MN的长度;
(3)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.
解答:解:(1)线段AC的长为AC=6-(-8)=14个单位长度;点M表示的数为-8+
[2-(-8)]=-3;
(2)当t=5时,点P表示的数为6-5×1=1,
点N表示的数为2-
[2-1]=1.5,
线段MN的长度为1.5-(-3)=4.5;
(3)①当点P在点A、B两点之间运动时,点P表示的数为6-t,点N表示的数为2+
[(6-t)-2]=4-
t,
线段MN的长度为4-
t-(-3)=7-
t;
②当点P运动到点B的左侧时,点P表示的数为6-t,点N表示的数为2-
[2-(6-t)]=4-
t,
线段MN的长度为|4-
t-(-3)|=|7-
t|.
故答案为:14,-3.
| 1 |
| 2 |
(2)当t=5时,点P表示的数为6-5×1=1,
点N表示的数为2-
| 1 |
| 2 |
线段MN的长度为1.5-(-3)=4.5;
(3)①当点P在点A、B两点之间运动时,点P表示的数为6-t,点N表示的数为2+
| 1 |
| 2 |
| 1 |
| 2 |
线段MN的长度为4-
| 1 |
| 2 |
| 1 |
| 2 |
②当点P运动到点B的左侧时,点P表示的数为6-t,点N表示的数为2-
| 1 |
| 2 |
| 1 |
| 2 |
线段MN的长度为|4-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:14,-3.
点评:本题考查了数轴与两点间的距离的应用,用到的知识点是数轴上两点之间的距离,关键是根据题意画出图形,注意分两种情况进行讨论.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
 已知一次函数y=kx-3的图象与正比例函数
已知一次函数y=kx-3的图象与正比例函数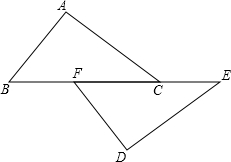 如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AC∥DF.求证:△ABC≌△DEF.
如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AC∥DF.求证:△ABC≌△DEF. 如图,线段AB=8cm,C是线段AB上一点,AC=3cm,M是AB的中点,N是AC的中点.
如图,线段AB=8cm,C是线段AB上一点,AC=3cm,M是AB的中点,N是AC的中点.