题目内容
20.如图,四边形ABCD是平行四边形,点P为AD边上一动点,连结CP并延长交BA的延长线于点M,过M作MN⊥BC,垂足是N,连结AN,NP,设点P运动时间为t(s),解答下列问题: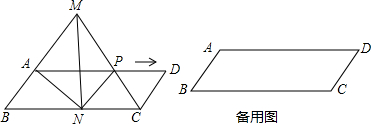
(1)若AD=6cm,CD=2cm,∠B=45°,点P从点A出发沿AD方向运动,速度为3cm/s,当t为何值时,四边形ACDM是平行四边形?
(2)在(1)的条件下,是否存在某一时刻t,使四边形ANPM是平行四边形?若存在,求出相应的t的值;若不存在,请说明理由.
分析 (1)连结AQ、MD,根据平行四边形的对角线互相平分得出AP=DP,代入求出即可;
(2)根据已知条件得出BN=MN,再根据BM=AB+AM,由边形ABCD是平行四边形,AP∥BC,当四边形ANPM是平行四边形时,得到PN∥AM,PN=AM,于是证得PN∥AB,又因为AP∥BN,得到四边形ABNP是平行四边形,PN=AB=2,BN=AP=3t,由勾股定理得出BN=MN=3t,由勾股定理得出结果.
解答  解:(1)如图1(1)连结AC、MD,
解:(1)如图1(1)连结AC、MD,
∵当AP=PD时,四边形ACDM是平行四边形,
∴3t=6-3t,
解得:t=1,
∴t=1s时,四边形ACDM是平行四边形;
(2)如图2∵MN⊥BC,
∴∠MNB=90°,
∵∠B=45°,
∴∠BMN=45°=∠B,
∴BN=MN,
∵BM=AB+AM,
∵四边形ABCD是平行四边形,
∴AP∥BC,
当四边形ANPM是平行四边形时,
PN∥AM,PN=AM,
∴PN∥AB,∵AP∥BN,
∴四边形ABNP是平行四边形,
∴PN=AB=2,BN=AP=3t,
∴AM=2,BM=3$\sqrt{2}$t,
∴$3\sqrt{2}t$=4,解得t=$\frac{2\sqrt{2}}{3}$,
当t=$\frac{2\sqrt{2}}{3}$s时,四边形ABNP是平行四边形.
若四边形ANPM是平行四边形,
则PN∥AM,PN=AN=CD,
∴AM平行且等于CD,
∴点P又为AD的中点,
∴3t=3,
∴t=1,
与当t=$\frac{2\sqrt{2}}{3}$s时,四边形ABNP是平行四边形相矛盾,
∴四边形ANPM不是平行四边形.
点评 本题考查了平行四边形的性质、解直角三角形、勾股定理的应用,主要考查学生综合运用性质进行推理和计算的能力,是一道综合性较强的题,有一定难度.

 阅读快车系列答案
阅读快车系列答案| A. | 0.12×109元 | B. | 1.2×108元 | C. | 1.2×107元 | D. | 0.12×108元 |
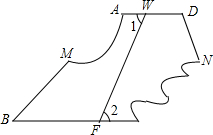 如图是一张四边形纸片ABCD被撕掉∠A和∠C后的剩余部分(∠A在左上角),量得∠1=∠2,∠B=45°,∠D=105°,在图中画出被撕掉的部分,并求原来∠A和∠C的度数.
如图是一张四边形纸片ABCD被撕掉∠A和∠C后的剩余部分(∠A在左上角),量得∠1=∠2,∠B=45°,∠D=105°,在图中画出被撕掉的部分,并求原来∠A和∠C的度数. 如图,O为矩形ABCD内的一点,且满足OB=OD,若O点到A点的距离用m表示,OB=n,试用含m、n的代数式表示OC=$\sqrt{2{n}^{2}-{m}^{2}}$.
如图,O为矩形ABCD内的一点,且满足OB=OD,若O点到A点的距离用m表示,OB=n,试用含m、n的代数式表示OC=$\sqrt{2{n}^{2}-{m}^{2}}$.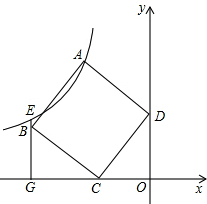 如图,正方形ABCD中,C(-3,0),D(0,4).过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.
如图,正方形ABCD中,C(-3,0),D(0,4).过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.