题目内容
如图，反比例函数y1=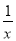
与二次函数y2=ax2+bx+c图象相交于A、B、C三个点，则函数y=ax2+bx-
+c的图象与X轴交点的个数是（ ）
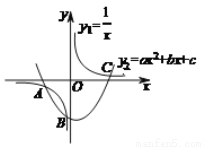
A. 3 B. 2 C. 1 D. 0
A 【解析】当时,得=ax²+bx+c,即ax²+bx?+c=0， ∵方程的解即反比例函数与二次函数=ax²+bx+c图象交点的横坐标， ∵反比例函数=与二次函数=ax²+bx+c图象相交于A. B. C三个点， ∴函数y=ax²+bx?+c的图象与x轴交点即是ax2+bx?1x+c=0的解， ∴函数y=ax²+bx?+c的图象与x轴交点的个数是3个， 故选A....
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
=_____．
某汽车厂计划半年内每月生产汽车20辆，由于另有任务，每月工作人数不一定相等，实际每月生产量与计划量相比情况如表（增加为正，减少为负）
月份 | 一 | 二 | 三 | 四 | 五 | 六 |
增减（辆） | +3 | ﹣2 | ﹣1 | +4 | +2 | ﹣5 |
①生产量最多的一月比生产量最少的一月多生产多少辆？
②半年内总产量是多少？比计划增加了还是减少了，增加或减少多少？
（1）9辆；（2）半年内总产量是121辆，比计划增加了1辆． 【解析】试题分析：①利用表中的最大数减去最小的数即可； ②半年内的计划总产量是20×6=120辆，然后求得六个月中的增减的总和即可判断． 试题解析：①生产量最多的一月比生产量最少的一月多生产4﹣（﹣5）=9（辆）； ②总产量是：20×6+（3﹣2﹣1+4+2﹣5）=121（辆）， 3﹣2﹣1+4+2﹣5=1...
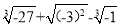