Question

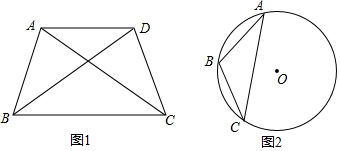
10．若一个四边形的一条对角线把四边形分成两个等腰三角形，且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍，我们把这条对角线叫做这个四边形的黄金线，这个四边形叫做黄金四边形．
（1）如图1，在四边形ABCD中，AB=AD=DC，对角线AC，BD都是黄金线，且AB＜AC，CD＜BD，求四边形ABCD各个内角的度数；
（2）如图2，点B是弧AC的中点，请在⊙O上找出所有的点D，使四边形ABCD的对角线AC是黄金线（要求：保留作图痕迹）；
（3）在黄金四边形ABCD中，AB=BC=CD，∠BAC=30°，求∠BAD的度数．

Answer 1

分析 （1））先由对角线AC是黄金线，可知△ABC是等腰三角形，分两种情况：①AB=BC，②AC=BC，第一种情况不成立，②设∠DAC=∠DCA=∠ABD=∠ADB=x°，则∠BDC=∠BCD=∠CAB=∠CBA=2x°，∠DAB=∠ADC=3x°，根据四边形内角和列等式可得x的值，计算各角的度数；
（2）①以A为圆心，AC为半径画弧，交圆O于D₁，
②以C为圆心，AC为半径画弧，交圆O于D₂，
③连接AD₁、CD₁、AD₂、CD₂；
（3）先根据∠BAC=30°，计算∠ABC=120°，
分情况进行讨论：
ⅰ）当AC为黄金线时，则AD=CD或AD=AC，根据等腰三角形的性质及黄金四边形定义进行计算即可；
ⅱ）当BD为黄金线时，分三种情况：
①当AB=AD时；②当AB=BD时，③当AD=BD时，分别讨论即可．

解答 解：（1）∵在四边形ABCD中，对角线AC是黄金线，
∴△ABC是等腰三角形，
∵AB＜AC，
∴AB=BC或AC=BC，
①当AB=BC时，
∵AB=AD=DC，
∴AB=BC=AD=DC，
又∵AC=AC，
∴△ABC≌△ADC，
此种情况不符合黄金四边形定义，
②AC=BC，
同理，BD=BC，
∴AC=BD=BC，易证得△ABD≌△DAC，△CAB≌△BDC，
∴∠DAC=∠DCA=∠ABD=∠ADB，∠BDC=∠BCD=∠CAB=∠CBA，
且∠DCA＜∠DCB，
∴∠DAC＜∠CAB
又由黄金四边形定义知：∠CAB=2∠DAC，
设∠DAC=∠DCA=∠ABD=∠ADB=x°，
则∠BDC=∠BCD=∠CAB=∠CBA=2x°，
∴∠DAB=∠ADC=3x°，
而四边形的内角和为360°，
∴∠DAB=∠ADC=108°，∠BCD=∠CBA=72°，
答：四边形ABCD各个内角的度数分别为108°，72°，108°，72°．
（2）由题意作图为：

（3）∵AB=BC，∠BAC=30°，
∴∠BCA=∠BAC=30°，∠ABC=120°，
ⅰ）当AC为黄金线时，
∴△ACD是等腰三角形，
∵AB=BC=CD，AC＞BC，
∴AD=CD或AD=AC，
当AD=CD时，则AB=BC=CD=AD，
又∵AC=AC，
∴△ABC≌△ADC，如图3，此种情况不符合黄金四边形定义，
∴AD≠CD，
当AD=AC时，由黄金四边形定义知，∠ACD=∠D=15°或60°，
此时∠BAD=180°（不合题意，舍去）或90°（不合题意，舍去）；
ⅱ）当BD为黄金线时，
∴△ABD是等腰三角形，
∵AB=BC=CD，
∴∠CBD=∠CDB，
①当AB=AD时，△BCD≌△BAD，
此种情况不符合黄金四边形定义；
②当AB=BD时，AB=BD=BC=CD，
∴△BCD是等边三角形，
∴∠CBD=60°，
∴∠A=30°或120°（不合题意，舍去），
∴∠ABC=180°（不合题意，舍去），
此种情况也不符合黄金四边形定义；
③当AD=BD时，设∠CBD=∠CDB=y°，则∠ABD=∠BAD=（2y）°或$（{\frac{y}{2}}）°$，
∵∠ABC=∠CBD+∠ABD=120°，
当∠ABD=2y°时，y=40，
∴∠BAD=2y=80°；
当$∠ABD=（{\frac{y}{2}}）°$时，y=80°，
∴$∠BAD=\frac{y}{2}=40°$；
由于∠ADB=180°-40°-40°=100°，
∠BDC=80°，
∴∠ADB+∠BDC=180°，
∴此种情况不能构成四边形，
综上所述：∠BAD的度数为80°．

点评 此题是圆与三角形、四边形的综合题，考查了等腰三角形的性质和判定、平行四边形的性质、菱形的性质以及含30°角的直角三角形的性质．此题难度较大，注意掌握数形结合思想与分类讨论思想的应用．